方程內容
沒有電流流動時的膜電位可用下式 來表示：
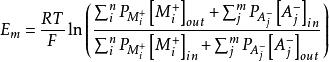戈德曼方程式中：F是法拉第常數，R是氣體常數，T是絕對溫度，P是通透常數，[ ]out、[ ]in分別是是細胞外，內的離子濃度。
主要推導公式 ：
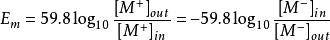戈德曼方程推導及套用
此式是在下列三種假定的條件下推導出來的：
（1）如在溶液中一樣，膜內離子也是在電場和濃度梯度的影響下移動的；
（2）緊貼膜的細胞內離子濃度和與其鄰接的溶液中的離子濃度相等；
戈德曼方程
戈德曼方程（3）膜內的電場梯度是均一的。因此上述方程式亦稱定電場方程（ D．E．Goldman 1943，A．L．Hodgkin和 B．Kotz1949）。式中的通透常數 的定義為μβRT/αF，單位是厘米/秒（ 是離子在膜內的移動度，β是膜和液相之間的分配率，α是膜的厚度）。
特別地，該方程只能適用於電荷數為±1的離子，因為本質上該方程一定程度上源於能斯特方程，這裡省略了z（離子電荷數），具體參見能斯特方程。
如果僅考慮鉀離子、鈉離子、氯離子對於膜電位的影響，那么該方程可以寫成下式 ：
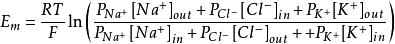戈德曼方程在37攝氏度的情況下，如果僅僅考慮一種帶正點或帶負電的離子，那么，該式可以簡化成 ：
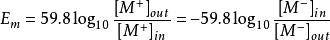戈德曼方程這就是上述的推導公式。
相關原理
根據方程式可以看到，離子帶正電時，膜外離子濃度與膜內離子濃度之比k取對數再乘常數得到結果。當k<1時（即膜外通透帶正電離子濃度>膜內通透帶正電離子濃度），取對數得負值，膜電位即為負值，靜息電位膜電位大概在-75mV左右。 值得注意的是，如果膜對該離子通透性幾乎為零則不能用該方程計算，也就是其對膜電位無影響，而推導公式中將通透常數約去的前提條件是該通透常數不為零，所以在用推導公式計算時，要注意該離子通透性是否為零。
該方程直觀地告指出了膜電位和膜內外離子的關係，實際電位發生的具體生物過程很複雜，可以近似地看做以下過程：
Ⅰ 假定細胞質膜對任何離子都不通透，此時膜電位無意義。但此時細胞內一種帶正電的離子多於細胞外的該種離子（比如鉀離子等）。
Ⅱ 細胞質膜只對這一種離子通透，受到濃度梯度影響，該種離子大量向外湧出，使得細胞內“想吸引的”正電荷和負電荷分離，這種分離使得膜內外產生了一種“壓”，即電壓或者說電位差，這就是膜電位。 其趨於內負外正。
Ⅲ 因為電壓的“力”（便於理解，且這樣稱之，實則道理很複雜）和濃度梯度產生的力相平衡，離子進入平衡狀態，形成內負外正的電位。
而內正外負的電位形成機理和以上同理。
