懸鏈線

懸鏈線（Catenary）是一種曲線，它的形狀因與懸在兩端的繩子因均勻引力作用下掉下來之形相似而名。適當選擇坐標系後，懸鏈線的方程是一個雙曲餘弦函式。

基本信息

• 中文名：懸鏈線
• 英文名：Catenary

• 屬性：曲線
• 方程：y=a cosh x/a

簡介

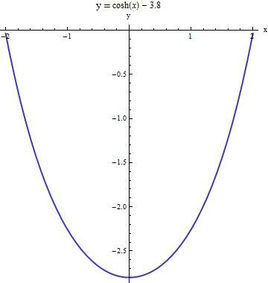
懸鏈線

懸鏈線是一種曲線，它的形狀因與懸在兩端的繩子因均勻引力作用下掉下來之形相似而名。它的公式為：
:y = a\cosh \frac
其中 ''a'' 是一個常數。

詳述

懸鏈線的證明
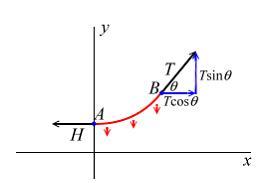
最低點處受水平向左的拉力H，右懸掛點處受一個斜向上的拉力T，設T和水平方向夾角為θ，繩子一半的質量為m,受力分析有：
Tsinθ=mg;
Tcosθ=H,
並且對於繩上任意一點有
tanθ=dy/dx=mg/H;
mg=ρs;
其中s是右半段繩子的長度,ρ是繩子密度,認為繩子截面積是1,帶入得微分方程dy/dx=ρs/H;利用弧長公式ds=√(1+dy^2/dx^2)*dx;所以s=∫√(1+dy^2/dx^2)*dx;
所以把s帶入微分方程得dy/dx=ρ∫√(1+dy^2/dx^2)*dx/H;.....(1)
對於(1)設p=dy/dx微分處理
得 p'=ρ/H*√(1+p^2)......(2)
p'=dp/dx;
對（2）分離常量求積分
∫dp/√(1+p^2)=∫ρ/H*dx
得ln【p+√(1+p^2)】=ρx/H+C
當x=0時，dy/dx=p=0;帶入得C=0；
整理得ln【p+√(1+p^2)】=ρx/H；
1+p^2=e^(2ρx/H)-2pe^(ρx/H)+p^2;
即p=【e^(ρx/H)-e^(-ρx/H)】/2=dy/dx;
dy得y=H/(2ρ)*【e^(ρx/H)+e^(-ρx/H)】 ；
如果令a=ρ/H的話
y=【e^(x/a)+e^(-x/a)】/(2a);