定義
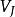快速小波轉換快速小波轉換它具有有限生成的正交多分辨分析（MRA）的裝置作為理論基礎。在那裡給出的術語中，選擇採樣率為每單位間隔2J的採樣比例J，並將給定信號f投影到空間 ;理論上通過計算標量產品。
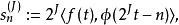快速小波轉換
快速小波轉換其中 是所選小波變換的縮放函式;實際上，在信號被高度過採樣的情況下，通過任何合適的採樣程式，所以
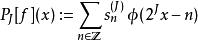快速小波轉換 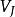快速小波轉換是 中的原始信號的正交投影或至少一些好的近似。
MRA的特徵在於其縮放序列
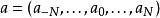快速小波轉換
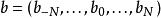快速小波轉換
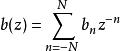快速小波轉換
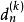快速小波轉換
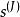快速小波轉換及其小波序列或（某些係數可能為零）。那些允許計算小波係數，至少某些範圍k = M，...， J-1，無需近似相應標量積中的積分。相反，在卷積和抽取運算元的幫助下，可以直接從第一個近似計算這些係數。
前項離散小波轉換
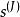快速小波轉換一個遞歸計算，從係數序列 開始並從k = J-1倒計數到某個M <J，
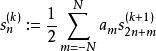快速小波轉換
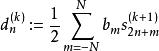快速小波轉換
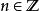快速小波轉換對於k = J-1，J-2，...，M和所有。在Z變換表示法中：
快速小波轉換
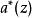快速小波轉換
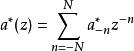快速小波轉換下採樣運算符（↓2）減少了一個無限序列，由其Z變換（簡稱為Laurent級數）給出了具有偶數索引的係數序列
。加星標的Laurent多項式表示伴隨濾波器，它具有時間反轉的伴隨係數（實數的伴隨是數字本身，它是一個複數的共軛，是一個實矩陣的轉置矩陣，是一個複雜矩陣的偶然伴隨）。
乘法是多項式乘法，相當於係數序列的卷積。
它遵循
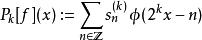快速小波轉換
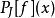快速小波轉換
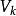快速小波轉換是原始信號f或至少第一近似值
到子空間的正交投影，即每單位間隔採樣率為2k。與第一近似的差異由下式給出：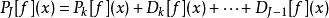
快速小波轉換其中差異或細節信號是從細節係數計算的
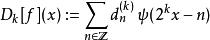快速小波轉換
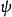快速小波轉換用 表示小波變換的母小波。
反離散小波轉換
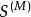快速小波轉換
快速小波轉換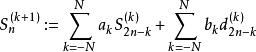
快速小波轉換利用 且M<J的一系列常數集合，以及由 ，k=M,1,...,J-1的差分集合可以導出有遞迴關係式的數學式 如下：
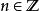快速小波轉換或是導入Z轉換，以k=J-1,J-2,...,M且 可改寫為
快速小波轉換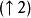
快速小波轉換其中 表示升高採樣操作子。
同時參閱
G. Beylkin, R. Coifman, V. Rokhlin, "Fast wavelet transforms and numerical algorithms" Comm. Pure Appl. Math., 44 (1991) pp. 141–183
