算符的復共軛算符,是由該算符中的復量換成共軛復量構成。在量子力學中,一個力學量由 厄米算符表示。一個厄米算符的厄米共軛算符,是由該厄米算符經過 轉置變換和 復共軛變換後得到的。 復共軛算符本身並不具有深刻的物理意義,它的主要描述的是 厄米共軛的中間過程的中間態。
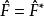 復共軛算符
復共軛算符復共軛:
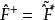 復共軛算符
復共軛算符厄米共軛:

一個算符的復共軛算符,是將該算符中的復量替換成該復量的共軛復量。
算符的復共軛算符,是由該算符中的復量換成共軛復量構成。在量子力學中,一個力學量由 厄米算符表示。一個厄米算符的厄米共軛算符,是由該厄米算符經過 轉置變換和 復共軛變換後得到的。 復共軛算符本身並不具有深刻的物理意義,它的主要描述的是 厄米共軛的中間過程的中間態。
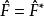 復共軛算符
復共軛算符復共軛:
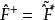 復共軛算符
復共軛算符厄米共軛:
在數學裡,作用於一個有限維的內積空間,自共軛矩陣。矩陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等;等價地說,表達自伴運算元的矩陣是...
定義 性質埃爾米特矩陣又稱自共軛矩陣、Hermite陣。Hermite陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等(然而矩陣A的共軛矩陣並...
基本信息 性質 序列用複變函數求解彈性力學問題的方法,主要用於求解平面問題。
正文 配圖 相關連線:如圖所示:對定理的證明過程,如圖所示:共軛調和函式:定義:如圖所示:定義的相關知識,如圖冊所示: 共軛調和函式關於定義的相關知識(4張)定理...的文章正式刊出,同年讓-羅貝爾·阿爾岡亦發表同類文章,而阿岡的複平面成了...
歷史 主要內容 產生 共軛複數 複數的輻角這裡 、 為任一復常數, 、 為任意波函式,就是說,如將某一函式抽出算符作用之外,需要對它取複數共軛。這是與線性算符本質的差別。性質 反么正算符 反么正算符 反線性算符 的Hermite共軛算符 的定義是: 反...
定義 性質 在時間反演變換的套用《上帝擲骰子嗎》 摘要 愛因斯坦:「一個人的價值,應該看他貢獻了什麼,而不是他取得了什麼。」 愛因斯坦說:「我不相信上帝是靠擲骰...
《上帝擲骰子嗎》 序 第一章 黃金時代 第二章 烏雲 第三章 火流星頁數: 242 頁簡介這些問題是:算符;量子力學的基本假設;角動量平方算符本徵方程的解;單電子原子體系Schrodinger方程的解以及波函式...和記號;空間群簡介;等效點系等。目錄第一章 算符1.1 算符的定義1.2...
結構化學問題選講 簡介 目錄從理論上構造了廣義光子湮滅算符的本徵態即所謂的雙光子相干態,因這種雙光子...這兩個正交相位分量的場算符的對易子必須等於上述正實數的2i倍等等)。為了...的對易子等於一個正的實數,也不要求電場和磁場這兩個正交相位分量的場算符...
光場壓縮態及其最新發展 多模壓縮態理論其具體發展過程該量的算符對其波函式的作用;波函式的模平方代表作為其變數的物理量出現...,物理量由滿足一定條件的、代表某種運算的算符表示;測量處於某一狀態的物理體系的某一物理量的操作,對應於代表該量的算符對其波函式的作用;測量的可能...
簡介 發展簡史 基本內容 具體套用 歷史背景