背景
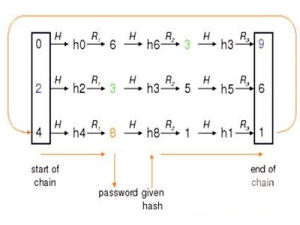
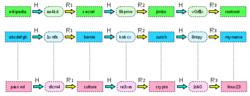圖1.彩虹表3倍減少查詢時間為了保證後台數據安全,現在的做法都是使用哈希算法對明文密碼進行加密後存儲。由於哈希算法不可逆向，因此由密碼逆向出明文運算就成了不可能。
起初黑客們通過字典窮舉的方法進行破解，這對簡單的密碼和簡單的密碼系統是可行的，但對於複雜的密碼和密碼系統，則會產生無窮大的字典。為了解決逆向破解的難題，黑客們就產生了彩虹表的技術。
為了減小規模太大的不足，黑客生成一個反查表僅存儲一小部分哈希值，而每條哈希值可逆向產生一個密碼長鏈（多個密碼）。雖然在鍊表中反查單個密文時需要更多的計算時間，但反查表本身要小得多，因此可以存儲更長密碼的哈希值。Rainbow table s是此鏈條技術的一種改進，並提供一種對被稱為“鏈碰撞”的問題的解決方案。其基於Martin Hellman理論(基於記憶體與時間的權重理論) 。
介紹
為了解決簡單的哈希鏈中的碰撞問題，彩虹表選用一系列相關的衰減函式R，…，R來代替原先的衰減函式R。這樣，如果兩個哈希鏈發生碰撞並且重合，那么它們的碰撞必定發生在相同的位置，從而它們的終點也將相同。這樣，我們可以通過後處理來對哈希鏈進行排序，從而找出並移除所有終點相同，因而可能是重複的鏈，並生成新的鏈來將整個表補充完整。這樣得到的表中的鏈可能有碰撞的部分，但它們不會發生鏈的重合，從而大幅降低了碰撞的次數。
採用衰減函式列代替衰減函式將改變查找的方式。因為給定的哈希值可能出現在哈希鏈中的任意位置，我們需要計算 k條不同的鏈：首先假定給定的哈希值出現在哈希鏈的最後一位（此時我們只需施加函式R），然後假定哈希值出現在哈希鏈的倒數第二位（此時我們依次施加函式R，H和R），依此類推，直至我們找到所需的密碼。注意，如果我們錯誤地假定了目標哈希值在哈希鏈中的位置，可能會得到一條與表中的鏈部分重合的鏈，從而產生誤報。
計算過程
假設我們有一個哈希方程H和一個有限的密碼集合P。我們需要預先計算出一個數據結構來幫我們決定哈希方程H的任意一個輸出結果 h是否可以通過密碼集合P裡面的一個元素 p經哈希函式H( p) = h得到。實現這一目的的最簡單的方法是計算出P集合內所有密碼 p的哈希值H( p)。但是這個方法要求Θ(|P| n)，（ n代表哈希函式H的一個輸出值的大小，對於較大的|P|， n會變得過高)位元組的空間來儲存結果。
哈希鏈可以用來減少對於儲存空間的需求。大致想法是通過定義一個 歸約函式（reduction function）R來影射散列值 h在集合P中對應的密碼 p。（注意，這裡的歸約函式並不是真正意義上哈希函式的反函式。)然後通過用歸約函式來替代哈希函式，形成交替的密碼和哈希值。例如，如果P是6個字元的密碼集合，而哈希值有32位長，那么他們形成的長鏈如下：
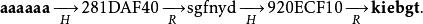彩虹表例子
已知一個32位的哈希值 -〉 獲得哈希值的最後4個字元。
對於歸約函式的唯一要求是，它需要能返回特定字元的純文本值。
為了生成查找表，我們從 初始密碼集合P中隨機選擇一個子集，對子集中的每個元素計算長度為 k的哈希鏈，然後 只保存每條哈希鏈的初始和末尾密碼。我們把初始密碼稱為 起點，把末尾密碼稱為 終點。在上述哈希鏈的例子中，"aaaaaa"和"kiebgt"即為起點和終點，而哈希鏈中的其他密碼或者哈希值均不會被保存。
現在，對於給定的哈希值 h我們來計算它的逆（即找到對應的密碼），從哈希值 h開始，我們通過依次施加函式R和H生成一個哈希鏈。如果哈希鏈的任何節點與查找表的某個 終點發生了碰撞，我們就可以找到與之對應的 起點，然後用它重建對應的哈希鏈。而這個哈希鏈很可能包含了 h，如果這樣的話，那么它的前驅節點即為我們要尋找的密碼 p。
例如，如果給定的哈希值為920ECF10，我們首先施加函式R：
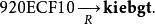彩虹表因為"kiebgt"就是我們查找表的一個 終點，所以我們找到對應的起始密碼"aaaaaa"，然後搜尋由它生成的哈希鏈直到找到920ECF10：
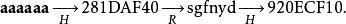彩虹表因此，目標密碼即為"sgfnyd"。
注意，這裡的哈希鏈並不 總是會包含我們要尋找的哈希值 h；很可能以 h開始的鏈會和 起點在 h鏈之後的某個查找鏈重合。例如，我們可以從FB107E70的哈希鏈中找到kiebgt：
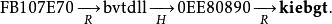彩虹表但FB107E70並不在以"aaaaaa"開頭的鏈中。這種情況被稱為 誤報。在這個例子中，我們可以忽略這個匹配然後繼續擴增 h鏈同時尋找下一個匹配。如果 h的哈希鏈在擴增到長度為 k後仍然沒有發生匹配，那么與之對應的密碼一定不在查找表的任何哈希鏈中。
查找表的內容並不依賴於查詢的哈希值。它是在一次性建立之後，被無修改的重複用於查找。增加鏈的長度可以減小表的規模，但同時也會增加查詢時間，這就是彩虹表空間換時間的折中策略。在單元鏈的最簡單情況下，查詢速度會非常快，但表也會非常大。一旦鏈變得更長，查找速度也會降下來，但表的規模變得更小了。
簡單的哈希鏈方法有很多缺陷。最嚴重的問題是，如果兩條鏈中的任何兩個點 碰撞（有同樣的值）了，他們後續的所有點都將重合，這將導致在付出了同樣的計算代價之後並不能使表儘可能多的覆蓋到密碼。由於鏈的前部並沒有整個的保存，這使得 碰撞不可能有效檢測到。例如，如果鏈3的第三個值和鏈7的第二個值重合了，那么這兩條鏈將覆蓋幾乎同樣的值，但他們的終點值卻不相同。哈希函式H本身不大可能產生碰撞，因為這就是它最重要的安全特性之一。但對於衰減函式R來說，由於他需要正確的覆蓋掉可能的明文（即之前討論的密碼），所以不會是抗碰撞的。
其他的困難是由選擇正確R函式的重要性導致的。選擇恆等映射作為函式R要比暴力搜尋好一點。只有當攻擊者明確知道明文的可能取值是什麼時，他/她才需要選擇一個好的R函式使得時間和空間花費在這些可能的明文上，而不是整個可能的密文空間。儘管把R的取值限定到可能的明文空間能帶來好處，但它的弊端是攻擊者選擇的用於生成哈希鏈的明文子集可能並不能覆蓋所有的可能明文空間。設計一個能匹配明文期望分布的R函式也非常困難。
