彈性和滯彈性
正文
彈性 一個物體在外力作用下改變其形狀和大小,當外力卸除後物體又可回復到原始的形狀和大小;這個特性稱為彈性。彈性(英文elastic)一詞源於希臘,十七世紀英國科學家玻意耳 (R.Boyle)賦予其科學意義並用到物理學中。彈性是各種工程材料的一項重要的物理性能(或列為力學性能),是材料科學的研究領域之一。固體的彈性理論是介於數學和物理學之間的一個分支學科,是近代力學的基礎(見金屬力學性能的表征)。胡克定律 固體彈性的近代理論是從英國胡克(R.Hooke)1660年的拉伸實驗開始的,其結論是伸長與力成正比。設一圓柱體橫截面積為A,兩個端面上施加沿軸向z的均勻拉力F,單位面積上的拉力σz=F/A稱為z方向的拉應力,圓柱體原始長度為l0,承受應力後的長度為l,則εz=(l-l0)/l0,稱為z方向的應變,胡克定律的數學表達式為
σz=Eεz
或 εz=σz/E (1)
其中E 是比例常數。
楊氏模量 英國物理學家楊 (T.Young)1807年用實驗測定了一些材料的E值,所以現在把E稱為楊氏模量或彈性模量。
泊松比 承受拉伸應力的圓棒除產生軸向伸長外還伴隨著徑向收縮。設原始直徑為r0,拉伸後直徑為r,則徑向應變εr=(r-r0)/r0與拉伸應力有下列關係
εr=-vσz/E (2)
這個關係是英國泊松 (S.D.Poisson)1829年發現的,所以現在把比例常數 v稱為泊松比。對於多數金屬材料v為1/4~1/3左右。
切變模量 在立方體的兩個相對的表面施加切應力τ,立方體將發生純剪下形變。其切應變以剪下角γ表示,則胡克定律可寫為
τ=Gγ 或 γ=τ/G (3)
比例常數G 稱為剪下彈性模量或切變模量或剛性模量。
壓縮模量 球狀物體在均勻靜水壓力P作用下,體積被均勻壓縮,體應變為ΔV/V,胡克定律可寫為
p=K(ΔV/V) (4)
K稱為體壓縮模量或壓縮係數。
各種彈性參數間的關係 楊氏模量、切變模量、體壓縮模量與泊松比等四個係數並不是獨立的,而存在以下聯繫
G=E/2(1+v) (5)
K=E/3(1-2v) (6)
因而在這四個係數中只有兩個是獨立的。
物質的彈性係數與原子間結合力有關,在單晶體中不同方向的原子結合力是不同的,因此彈性係數也是不相同的。精確測量這些彈性係數的取向關係及溫度關係,與固體理論的計算進行比較,可以研究各種晶體結合鍵的規律。測量高壓下的體壓縮模量可以研究固體狀態方程。
彈性極限 應力正比於應變的比例關係(胡克定律)保持不變的最大應力稱為比例極限。彈性極限是使材料開始發生範性形變的應力。工程上往往採用比例極限或屈服強度來代替彈性極限。
彈性模量的測定 彈性模量表征各種材料抵抗變形的能力,是工程設計中十分重要的一個參數。工業上多是利用物理方法測定,如懸掛法、彎曲共振頻率測量法、壓電石英複合振子法及超聲脈衝法等。
滯彈性 在低於彈性極限的應力範圍內,實際固體的應力和應變不是單值對應關係,往往有一個時間的滯後現象(見圖),這種特性稱為滯彈性,這個詞是美國人曾訥 (C.Zener)1947年首先套用的。目前滯彈性已成為材料科學的一個研究領域。
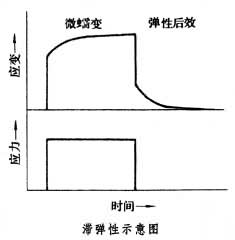 彈性和滯彈性
彈性和滯彈性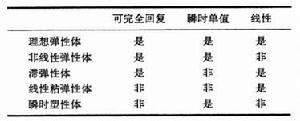 彈性和滯彈性
彈性和滯彈性tgφ=Δω掦/【1+ω掦)2】式中掦=(τσ+τε)1/2
為平均弛豫時間;Δ為弛豫強度(無量綱);ω為振動頻率。
參考書目
錢偉長、葉開源:《彈性力學》,科學出版社,北京,1956。
C.Zener,Elasticity and Anelasticity of Metals,Chicago University Press,Chicago,1948.
