點列
點列的弱收斂
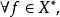弱收斂定義1 設X為賦范線性空間，x，x∈X，若對 有
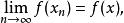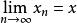弱收斂
弱收斂則稱{x} 弱收斂於x，記作w- .
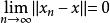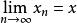弱收斂 弱收斂註：設X為賦范線性空間，x，x∈X，當 時，稱{x} 強收斂於x，記作s- .
性質
1.由點列強收斂可推出其弱收斂。
證明：由
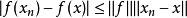弱收斂可證。並且強極限存在時必等於其弱極限，反之卻不然。
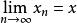弱收斂2.設X為賦范線性空間，x，x∈X，則w- ，若且唯若
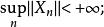弱收斂（1）
（2）存在X*上一個稠密集Y，使得
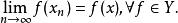弱收斂3.設X為一致凸的賦范線性空間，則X中的點列{x}強收斂於x的充要條件是{x}弱收斂於x，且有
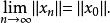弱收斂運算元列
運算元列的弱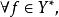收斂
弱收斂定義2 設X、Y均為賦范線性空間，T∈B(X→Y)，若對 有
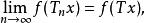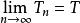弱收斂
弱收斂則稱{T}按 弱運算元拓撲收斂於T，記作w- .
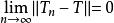弱收斂註：1.設X、Y均為賦范線性空間，T∈B(X→Y)，當 時，稱{T} 一致 收斂於T；
弱收斂2.設X、Y均為賦范線性空間，T∈B(X→Y)，若對 有
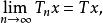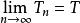弱收斂 弱收斂則稱{T}按 強運算元拓撲 收斂於T，記作s- .
性質
一致收斂蘊含了強運算元拓撲收斂，強運算元拓撲收斂蘊含了弱運算元拓撲收斂。
泛函列
泛函列的弱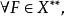收斂
弱收斂定義3 設X為賦范線性空間，X*為其對偶空間，f，f ∈X*，若對 有
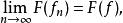弱收斂則稱{f} 弱 收斂於T.
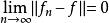弱收斂
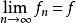弱收斂註：1.設X為賦范線性空間，X*為其對偶空間，f，f ∈X*，當 時，稱{f} 強收斂於f，記作s- ；
弱收斂2.設X為賦范線性空間，X*為其對偶空間，f，f ∈X*，若對 有
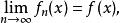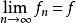弱收斂 弱收斂則稱{f} 弱* 收斂於f，記作w*- .
性質
當X為自反空間時，{f}弱收斂與{f}弱*收斂等價。
設X為Banach空間，f，f ∈X*，則{f}弱*收斂於f，若且唯若
1.當X為自反空間時，{f}弱收斂與{f}弱*收斂等價。
2.設X為Banach空間，f，f ∈X*，則{f}弱*收斂於f，若且唯若
（1）
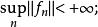弱收斂（2）存在X上的稠密集X，使得
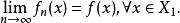弱收斂