廣勾股定理
勾股定理反映了直角三角形三邊之間的度量關係,即“斜邊的平方等於兩直角邊的平方之和”.如果不是直角三角形,而是銳角或鈍角三角形,那么它們的三邊之間存在怎樣的度量關係呢?這就涉及到廣勾股定理了.
廣勾股定理:在任一三角形中,
(1)銳角對邊的平方,等於其他兩邊之平方和,減去這兩邊中的一邊和另一邊在這邊上的射影乘積的兩倍.
(2)鈍角對邊的平方等於其他兩邊的平方和,加上這兩邊中的一邊與另一邊在這邊上的射影乘積的兩倍.
證明過程
 廣勾股定理
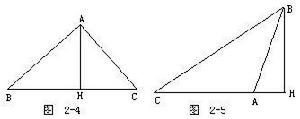
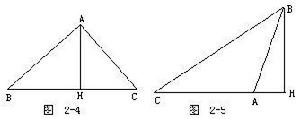
廣勾股定理(1)設△ABC中,BC是銳角A的對邊(圖2-4).作BH⊥AC於H,因為
AB2=BH2+AH2,
BC2=BH2+CH2,
所以,
BC2-AB2=CH2-AH2.
∴BC2=AB2+CH2-AH2. (1)
但是CH2=(AC-AH)2
=AC2-2AC·AH+AH2. (2)
將(2)代入(1)就得到
BC2=AB2+AC2-2AC·AH.
(當H在AC邊的延長線上時,結論是一樣的.)