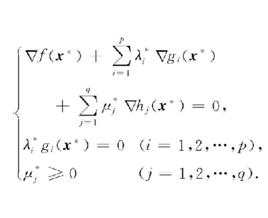基本介紹
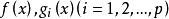 庫恩塔克條件
庫恩塔克條件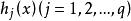 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件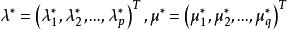 庫恩塔克條件
庫恩塔克條件庫恩-塔克爾條件(Kuhn-Tucker condition)是判定約束非線性規劃問題的某可行點為極小點的必要條件。對於凸規劃來說,則是判別極小點的充分必要條件。對於約束非線性規劃問題(NP)(參見“非線性規劃”),設其中和在R的某一開集上一階連續可微,是問題的極小點,且是約束條件的正則點,則存在向量及μ=(μ,μ,…,μ),使得
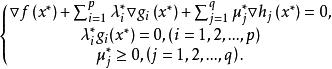 庫恩塔克條件
庫恩塔克條件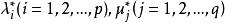 庫恩塔克條件
庫恩塔克條件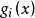 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件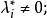 庫恩塔克條件
庫恩塔克條件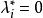 庫恩塔克條件
庫恩塔克條件此即為所考慮約束非線性規劃問題(NP)的 庫恩-塔克爾條件,也稱一階必要條件,稱為 庫恩-塔克爾乘子。由上述庫恩-塔克爾條件可知,只有當在點為起作用約束時,可以有否則,。1951年,庫恩(H.W.Kuhn)和塔克爾(A.W.Tucker)證明了這一條件,為非線性規劃奠定了重要理論基礎 。
相關介紹
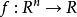 庫恩塔克條件
庫恩塔克條件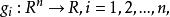 庫恩塔克條件
庫恩塔克條件令及考慮如下最最佳化問題:
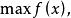 庫恩塔克條件
庫恩塔克條件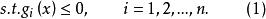 庫恩塔克條件
庫恩塔克條件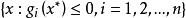 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件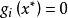 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件點集叫做 可行集。如果在某一特定的,有,則稱第個約束是起作用的約束; 否則就稱第個約束不起作用,或是一鬆弛的約束。
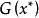 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件令為在處起作用的約束的梯度集:
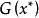 庫恩塔克條件
庫恩塔克條件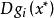 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件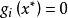 庫恩塔克條件
庫恩塔克條件={對於所有的滿足}。
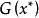 庫恩塔克條件
庫恩塔克條件如果向量集是線性無關的,那么稱約束包成立 。
庫恩一塔克定理
 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件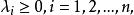 庫恩塔克條件
庫恩塔克條件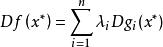 庫恩塔克條件
庫恩塔克條件如果是(1)的解且約束包在成立。那么存在一組庫恩一塔克乘子使得。進一步地,有互補鬆弛條件:
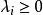 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件對於所有的;
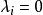 庫恩塔克條件
庫恩塔克條件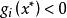 庫恩塔克條件
庫恩塔克條件當。
比較庫恩-塔克定理與拉格朗日定理,可以發現主要區別在於庫恩-塔克乘子的符號是非負的,而拉格朗日乘子可以是任意一個數,這一增加的信息優勢可以是很有用的。當然,庫恩-塔克定理僅是極大值條件的一個必要條件,然而,在一個重要的情形里,它是必要且充分的。
庫恩一塔克充分條件
 庫恩塔克條件
庫恩塔克條件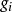 庫恩塔克條件
庫恩塔克條件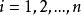 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件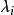 庫恩塔克條件
庫恩塔克條件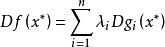 庫恩塔克條件
庫恩塔克條件 庫恩塔克條件
庫恩塔克條件假設是一凹函式,是一凸函式,,令為一可行點,並假設我們能夠找到非負數值,使得。那么是極大化問題(1)的解 。