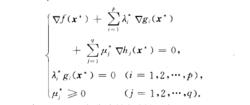 庫恩一塔克爾條件
庫恩一塔克爾條件庫恩一塔克爾條件(Kuhn-Tucker condition)判定約束非線性規劃問題的某可行點為極小點的必要條件.對於凸規劃來說,則是判別極小點的充分必要條件.對於約束非線性規劃問題(NP)參見“非線性規劃”),設其中f<x),g;(x) (i=1,2,...} p)和h;(x)<j=1,2,"..}q}在R”的某一開集上一階連續可微,x‘是問題的極小點,且是約束條件的正則點,則存在向量入‘一(可,叮,…,形}T及}.一<f}o ,可,…, I-r' )Tn,使得
此即為所考慮約束非線性規劃問題(NP)的庫恩一塔克爾條件,也稱一階必要條件..};" (i=1,2,...}},)及f}," <7=1,2,"..}q}稱為庫恩一塔克爾乘子.由上述庫恩一塔克爾條件可知,只有當gr(x)在x‘點為起作用約束時,可以有不並。;否則,不= 0. 1951年,庫恩(Kuhn,H. W.)和塔克爾(Tucker , A. W.)證明了這 一條件,為非線性規劃奠定了重要理論基礎.
