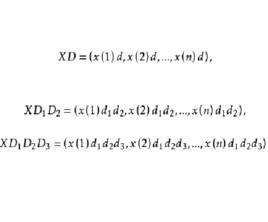定義
設X為系統行為數據序列,D為作用於X的運算元,X經過運算元D作用後所得序列記為
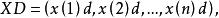 序列運算元
序列運算元稱D為 序列運算元,稱XD為 一階運算元作用序列。
 序列運算元
序列運算元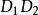 序列運算元
序列運算元序列運算元的作用可以進行多次,相應地,若皆為 序列運算元,我們稱為 二階運算元,並稱
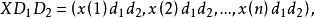 序列運算元
序列運算元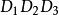 序列運算元
序列運算元為 二階運算元作用序列。同理稱為 三階序列運算元,並稱
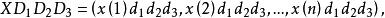 序列運算元
序列運算元為 三階運算元作用序列,等等 。
緩衝運算元三公理
序列運算元D可根據原始序列受衝擊波干擾的情況進行適當定義。
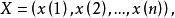 序列運算元
序列運算元定義1設序列
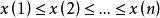 序列運算元
序列運算元1. 若,則稱X為增長序列,
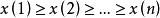 序列運算元
序列運算元2. 若,則稱X為衰減序列,
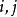 序列運算元
序列運算元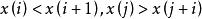 序列運算元
序列運算元3. 若存在,使得,則稱X為振盪序列。 ·
公理1(不動點公理) 設X為系統行為數據序列,D為序列運算元,則D滿足
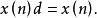 序列運算元
序列運算元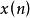 序列運算元
序列運算元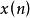 序列運算元
序列運算元不動點公理限定在序列運算元作用下,系統行為數據序列中的數據保持不變,即運用序列運算元對系統行為數據進行調整,不改變這一即成事實。
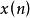 序列運算元
序列運算元根據定性分析的結論,亦可使以前的若干個數據在序列運算元作用下保持不變。例如,令
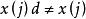 序列運算元
序列運算元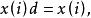 序列運算元
序列運算元且
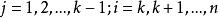 序列運算元
序列運算元其中。
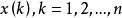 序列運算元
序列運算元公理2(信息充分利用公理) 系統行為數據序列X中的每一個數據都應充分地參與運算元作用的全過程。
信息充分利用公理限定任何序列運算元都應以現有序列中的信息為基礎進行定義,不允許拋開原始數據另搞一套。
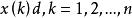 序列運算元
序列運算元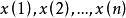 序列運算元
序列運算元公理3(解析化、規範化公理) 任意的,皆可由一個統一的的初等解析式表達。
公理3要求由系統行為數據序列得到運算元作用序列的程式清晰、規範、統一且儘可能簡化,以便於計算出運算元作用序列並使計算易於在計算機上實現。
定義2 稱上述三個公理為緩衝運算元三公理,滿足緩衝運算元三公理的序列運算元稱為 緩衝運算元,一階、二階、三階……緩衝運算元作用序列稱為一階、二階、三階……緩衝序列。
定義3 設X為原始數據序列,D為緩衝運算元,當X分別為增長序列、衰減序列或振盪序列時:
1. 若緩衝序列XD比原始序列X的增長速度(或衰減速度)減緩或振幅減小,我們稱緩衝運算元D為弱化運算元;
2. 若緩衝序列XD比原始序列X的增長速度(或衰減速度)加快或振幅增大,則稱緩衝運算元D為強化運算元 。
緩衝運算元的性質
定理1 設X為單調增長序列,XD為其緩衝序列,則有
 序列運算元
序列運算元1. D為弱化運算元;
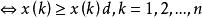 序列運算元
序列運算元2. D為強化運算元。
即單調增長序列在弱化運算元作用下數據膨脹,在強化運算元作用下數據萎縮。
定理2 設X為單調衰減序列,XD為其緩衝序列,則有
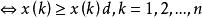 序列運算元
序列運算元1. D為弱化運算元;
 序列運算元
序列運算元2. D為強化運算元。
即單調衰減序列在弱化運算元作用下數據萎縮,在強化運算元作用下數據膨脹.
定理3 設X為振盪序列,XD為其緩衝序列,則有
1.若D為弱化運算元,則
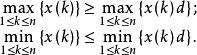 序列運算元
序列運算元2.若D為強化運算元,則
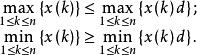 序列運算元
序列運算元實用緩衝運算元的構造
定理4 設原始數據序列
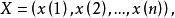 序列運算元
序列運算元令
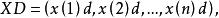 序列運算元
序列運算元其中
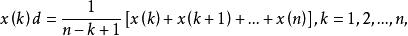 序列運算元
序列運算元則當X為單調增長序列、單調衰減序列或振盪序列時,D皆為弱化運算元。
下面的推論進一步刻化了弱化運算元D的性質:
推論1 對於定理4中定義的弱化運算元D,令
 序列運算元
序列運算元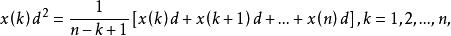 序列運算元
序列運算元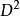 序列運算元
序列運算元則對於單調增長、單調衰減或振盪序列,皆為二階弱化運算元。
定理5 設原始序列和其緩衝序列分別為
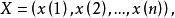 序列運算元
序列運算元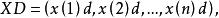 序列運算元
序列運算元其中
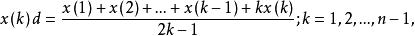 序列運算元
序列運算元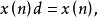 序列運算元
序列運算元則當X為單調增長序列或單調衰減亭列時,D皆為強化運算元。
推論2 設D為定理5中定義的強化運算元,令
 序列運算元
序列運算元其中
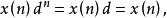 序列運算元
序列運算元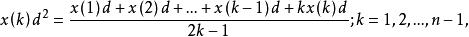 序列運算元
序列運算元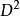 序列運算元
序列運算元則對於單調增長序列和單調衰減序列皆為二階強化運算元。
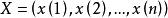 序列運算元
序列運算元定理6 設,令
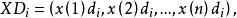 序列運算元
序列運算元其中
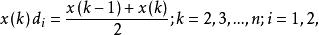 序列運算元
序列運算元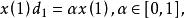 序列運算元
序列運算元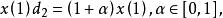 序列運算元
序列運算元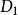 序列運算元
序列運算元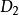 序列運算元
序列運算元則對單調增長序列為強化運算元,對單調衰減序列為強化運算元.
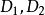 序列運算元
序列運算元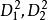 序列運算元
序列運算元推論3 對於定理6中定義的,則分別為單調增長、單調衰減序列的二階強化運算元。
當然,我們還可以考慮構造其它形式的實用緩衝運算元。緩衝運算元不僅可以用於灰色系統建模,而且還可以用於其它各種模型建模,通常在建模之前根據定性分析結論對原始數據序列施以緩衝運算元,淡化或消除衝擊擾動對系統行為數據序列的影響,往往會收到預期的效果 。