基本介紹
Richard Games採用了一種全新的思想理解m序列的周期互相關函式。設GF(2) 是有限域GF(2)上的向量空間,PG(n-1,2)是GF(2) 上的有限射影幾何。我們知道任意一個m序列都可以表示成
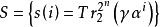 幾何序列
幾何序列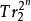 幾何序列
幾何序列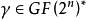 幾何序列
幾何序列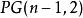 幾何序列
幾何序列的形式,這裡α是GF(2 )的本原元, 是GF(2 )到GF(2)上的跡函式, 。Games證明了m序列S和 上的超平面
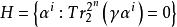 幾何序列
幾何序列是一一對應的。這樣,Games把m序列看成一個有限射影幾何上的超平面,則m序列的周期互相關函式等價於超曲面的交點數,然後利用有限射影幾何的理論計算出了一些m序列的周期互相關函式。
Klapper,Chan和Goresky在Games的基礎上研究了一類稱為幾何序列的自相關和互相關函式。下面我們給出幾何序列的定義 。
*幾何序列還有一種定義:稱環A的元素序列(u)是幾何序列,如果存在A的元素a,使得對任一非零自然數n,有u=au=ua. 在此條件下,對任一自然數n,有u=a b,其中b=u,反之,如果ab=ba,則由前面關係定義的序列(u)是幾何序列,它稱為以a為公比、以b為首項的幾何序列 。
Ⅰ型幾何序列
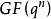 幾何序列
幾何序列定義 設n是正整數,q是素數p的方冪,α是有限域 的本原元,
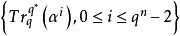 幾何序列
幾何序列為q元m序列,f是從GF(q)到GF(2)的任意非線性函式,稱序列
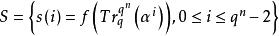 幾何序列
幾何序列為 Ⅰ型幾何序列。
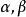 幾何序列
幾何序列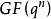 幾何序列
幾何序列定義2 設 是有限域 的兩個本原元,
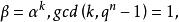 幾何序列
幾何序列f,g是從GF(q)到GF(2)的任意非線性函式,
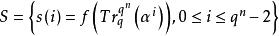 幾何序列
幾何序列和
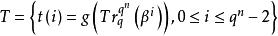 幾何序列
幾何序列是兩個Ⅰ型幾何序列。若是
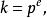 幾何序列
幾何序列則稱序列T和序列S是線性相關的;若
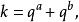 幾何序列
幾何序列稱序列T和序列S是二次相關的。
Klapper等人給出了線性相關和二次相關的Ⅰ型幾何序列的互相關函式。但是它們只是下面要介紹的Ⅱ型幾何序列的特例,所以這裡省略。
Ⅱ型幾何序列
下面我們研究另外一種形式的幾何序列,它既可以看作是定義1中幾何序列的特殊形式,也可以看作是它的推廣形式。
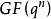 幾何序列
幾何序列定義3 設q是素數p的冪,m|n,α是 的本原元,
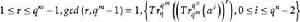 幾何序列
幾何序列是有限域GF(q)上的GMW序列,f是GF(q)到GF(2)的任意非線性函式,稱
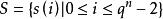 幾何序列
幾何序列為 Ⅱ型幾何序列,其中
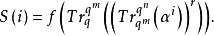 幾何序列
幾何序列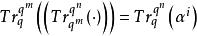 幾何序列
幾何序列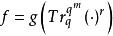 幾何序列
幾何序列特別地,當r=l時,由於 ,所以S就退化為Ⅰ型幾何序列;在Ⅰ型幾何序列中,若取 ,就是Ⅱ型幾何序列 。