簡介
水平集方法( Level Set Method) 是一種用於界面追蹤和形狀建模的數值技術。水平集方法的優點是可以在笛卡爾格線(Cartesian grid)上對演化中的曲線曲面進行數值計算而不必對曲線曲面參數化(這是所謂的 歐拉法(Eulerian approach))。水平集方法的另一個優點是可以方便的追蹤物體的拓撲結構改變。例如當物體的形狀一分為二,產生空洞,或者相反的這些操作。所有這些使得水平集方法成為隨時間變化的物體建模的有力工具,例如膨脹中的氣囊, 掉落到水中的油滴。
水平集方法
 水平集方法
水平集方法 水平集方法
水平集方法 水平集方法
水平集方法 水平集方法
水平集方法理解水平集方法的最簡單有效地方式是先學習相應的例子,然後學習技術性很強的定義。右側的圖片示例了水平集的幾個重要思想。在左上角有一個形狀--由一個良性邊界包圍的有界區域。在它的下面,紅色的曲面是相應的水平集函式的圖像,的某個水平面決定了左上角的形狀,假設其中的藍色平面即為x-y平面,則形狀的邊界可以表示為的零水平集,並且該形狀是平面上滿足大於等於零的點的集合。
在上面的一行,形狀改變其拓撲結構,分裂為兩個形狀。如果用邊界曲線參數表示形狀,這一演化過程是很難表達的。這需要一個算法能夠檢測到形狀分裂的時刻,然後為分裂後的曲線構造新的參數。另一方面,從下面的一行可以看出水平集函式僅僅是向下方移動了一點。由於在直接法中我們需要監視所有形狀可能發生的變化情況,水平集方法處理形狀曲線要比直接方法容易得多。
 水平集方法
水平集方法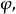 水平集方法
水平集方法在二維情況下,水平集方法意味著將平面上的閉曲線(正如示例中的形狀)表示為二維輔助函式的零水平集
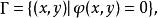 水平集方法
水平集方法 水平集方法
水平集方法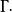 水平集方法
水平集方法 水平集方法
水平集方法 水平集方法
水平集方法 水平集方法
水平集方法然後通過函式 隱式的處理曲線這一函式便被叫做 水平集函式。假設在曲線的內部取正值,在曲線的外部取負值。
水平集方程
如果零水平集以速度 v沿著其法線運動,這一運動可以表示為水平集函式的 哈密頓-雅可比方程( Hamilton-Jacobi equation):
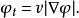 水平集方法
水平集方法這是一個偏微分方程,並且可以求得數值解,例如可以在笛卡爾格線上採用有限差分法。
然而,水平集方程的數值解需要複雜的技術。簡單的有限差分法會很快導致不收斂。迎風方法,諸如Godunov方法前進緩慢;然而在水平對流場中,水平集方法不保持水平集的體積和形狀的守恆。
歷史
美國數學家Stanley Osher和James Sethian於20世紀80年代開發出了水平集方法。這一方法在許多學科廣泛使用,例如圖像處理,計算幾何,最最佳化和計算流體力學。
大量的有關水平集數據結構被開發出來,使得水平集方法在計算中的套用變得更加方便。
參閱
•流體體積法
