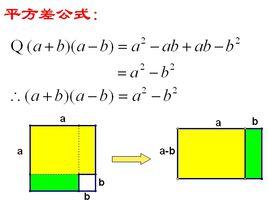
平方差公式
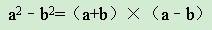 平方公式
平方公式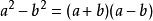 平方差
平方差兩個數a和b的平方之差, 就是他們的平方差利用平方差公式可以分解因式:
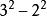 平方差
平方差例如:
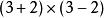 平方差
平方差=
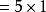 平方差
平方差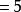 平方差
平方差勾股定理也可以描述為:直角三角形的斜邊和另一邊的長度的平方差恰為第三邊的長度的平方。
斐波那契(LeonardoFibonacci)曾解決了一個很著名的關於平方差的問題:求三個互不相同的正整數a>b>c, 使得相鄰兩數的平方差皆相等,
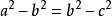 平方差
平方差即.
完全平方公式
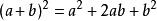 平方差
平方差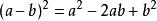 平方差
平方差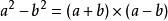 平方差
平方差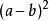 平方差
平方差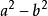 平方差
平方差兩數和(或差)的平方,等於它們的平方和,加上(或減去)它們的積的2倍即完全平方公式。與都叫做完全平方公式.為了區別,我們把前者叫做兩數和的完全平方公式,後者叫做兩數差的完全平方公式。這兩個公式的結構特徵是:左邊是兩個相同的二項式相乘,右邊是三項式,是左邊二中兩項的平方和,加上(這兩項相加時)或減去(這兩項相減時)這兩項乘積的2倍;公式中的字母可以表示具體的數(正數或負數),也可以表示單項式或多項式等代數式.平方差公式:當乘式是兩個數之和以及這兩個數之差相乘時,積是二項式.這是因為具備這樣特點的兩個二項式相乘,積的四項中,會出現互為相反數的兩項,合併這兩項的結果為零,於是就剩下兩項了.而它們的積等於乘式中這兩個數的平方差,即例:完全平方差平方差
普通情況
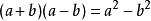 平方差
平方差舉例:
101×99
=(100+1)X(100-1)
=100²-1
=10000-1
=9999
驗證方法
主驗證
平方差可利用因式分解及分配律來驗證 。先設a及b。
ba-ab=0
那即是ab=ba,同時運用了環的原理。把這公式代入:
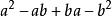 平方差
平方差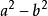 平方差
平方差若上列公式是的話,就得到以下公式:
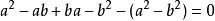 平方差
平方差以上運用了r-r=0,也即是兩方是相等,就得到:
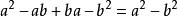 平方差
平方差註:a²-ab+ba-b²=(a-b)(a+b)
方格驗證
平方差能使用表格方式來驗證。
| x) | a | +b |
| a | a² | +ab |
| -b | -ab | -b² |
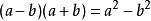 平方差
平方差這樣可驗證出
幾何驗證
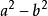 平方差
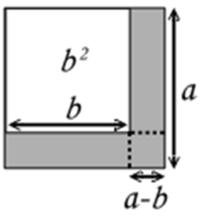
平方差平方差可透過一個普通的平面圖表驗證出來。右圖中,是正方形a²減去正方形b²,那即是。透過平方差,計算出陰影部分的面積就是(a+b)(a-b)。
方法一
 平方差
平方差根據右圖,可先將陰影部分分割成三部分,分別為:
•b(a-b)
•(a-b)²
•b(a-b)
然後,將三部分加起:
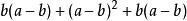 平方差
平方差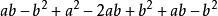 平方差
平方差=
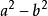 平方差
平方差=
註:運用了差平方。
方法二
與方法一差不多,先將陰影部分分割為兩部分,分別為:
1、a(a-b)
2、b(a-b)
然後,將1、2相加:
a(a-b)+b(a-b)
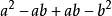 平方差
平方差=
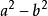 平方差
平方差=
延伸
n次方差公式
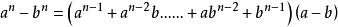 平方差
平方差使用條件:n 為大於0的自然數(正整數)
 平方差
平方差 平方差
平方差或
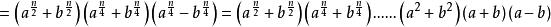 平方差
平方差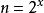 平方差
平方差使用條件: ,且x為大於0的自然數(正整數)
(此公式經常 逆用)