基本介紹
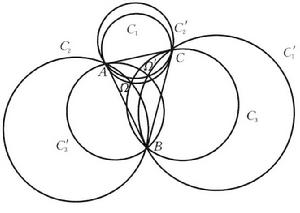
布羅卡爾點(Brocard point)是刻畫三個圓相關位置的特殊點，在△ABC中，設C是過C而切AB於A的圓，C是過A而切BC於B的圓，C是過B而切CA於C的圓；又設C′是過C而切AB於B的圓，C′是過A而切BC於C的圓，C′是過B而切CA於A的圓，則C，C，C三個圓交於一點Ω；C′，C′，C′三個圓交於一點Ω′，點Ω和Ω′稱為△ABC的 布羅卡爾點，Ω稱為 正布羅卡爾點，Ω′稱為 負布羅卡爾點，Ω與Ω′是△ABC的等角共軛點。布羅卡爾點具有性質：
∠ΩAB=∠ΩBC=∠ΩCA；
∠Ω′AC=∠Ω′CB=∠Ω′BA.
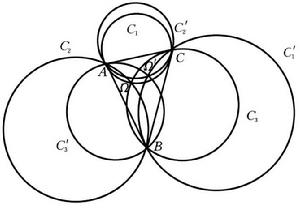圖1布羅卡爾點當這六個角相等時，稱為△ABC的 布羅卡爾角。研究布羅卡爾點的有關性質的幾何內容稱為 布羅卡爾幾何，點Ω和Ω′是由克雷爾(A.L.Crelle)首先發現的，但當時並未引起人們重視，布羅卡爾(P.R.J.B.H.Brocard)於1881年向法國科學進步協會提交的論文《三角平面一個新圓的研究》宣布布羅卡爾圓的重新發現，並由此產生布羅卡爾點、布羅卡爾三角形等概念。
例題解析
【例1】 (1)證明：△ABC記憶體在這樣的點P，使得∠ABP =∠CAP =∠BCP。
(2)在△ABC的邊上向形外作相似於它的△CAB，△CAB和△CAB(全部四個三角形第一個頂點的角相等，依此類推)，證明：直線AA，BB和CC相交於一點，並且這個點與問題(1)中的點P重合。點P稱為△ABC的布羅卡爾點。類似可證，還存在第二個布羅卡爾點Q，對於它滿足∠BAQ=∠ACQ=∠CBQ。
提示 立刻解問題(2)。首先證明，直線AA，BB和CC相交於一點，設△ABC和△ABC的外接圓相交於點O，則
∠(BO，OA) =∠(BO，OC) +∠(OC，OA) =∠(BA，AC) +∠(CB，BA) =∠(BA，AC) +∠(CB，BA) =∠(CB，AC)
即△ABC的外接圓也過點O，所以
∠(AO，OA) =∠(AO，OB) +∠(BO，OA) =∠(AC，CB) +∠(BC，CA) = 0°
也就是直線AA過點O，類似可證，直線BB和CC過點O。
現在證明，點O與所求的點P重合，因為∠BAP=∠A-∠CAP，所以等式∠ABP =∠CAP等價於等式∠BAP+∠ABP=∠A，即∠APB =∠B+∠C，對於點O最後的等式是顯然的，因為它位於△ABC的外接圓上。
【例2】(1)過△ABC的布羅卡爾點引直線AP，BP和CP，交外接圓於點A，B和C，證明:△ABC≌△B CA。
(2)△ABC內接於圓S，證明：使直線PA，PB和PC與圓s的交點形成的三角形與△ABC全等的不同的點P不少於8個(假設直線PA，PB和PC與圓的交點不同於點A，B和C)。
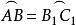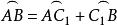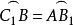布羅卡爾點
布羅卡爾點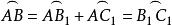
布羅卡爾點
布羅卡爾點提示 (1)我們證明， ，即AB= BC，實際上， ，而 ，所以 。
(2)我們認為△ABC和△ABC內接於一個圓中，並且△ABC是固定的，而△ABC旋轉，直線AA，BB和CC交於一點不比△ABC的一個位置多，在此情況下可以產生12個不同的△ABC類:△ABC和△ABC可以使旋轉或軸對稱結合在一起；除此之外，三角形頂點的記號A，B和C可以對照六種不同的方法。
這12類不同三角形中有4類永遠不能給出所求的點P，對於一致有向三角形的除去△ABC≌△ABC，△ABC≌△CBA和△ABC≌△BAC的情況(例如，在△ABC≌△ABC的情況，點P是直線BC與BC的交點且對圓切於點A = A；△ABC和△ABC此時重合)，對於相反定向的三角形除去
△ABC≌△ABC的情況(在這種情況下AA// BB// CC)。
註：布羅卡爾點對應於相反定向三角形；對第一布羅卡爾點△ABC≌△BCA，而對第二布羅卡爾點△ABC≌△CAB
