基本概念
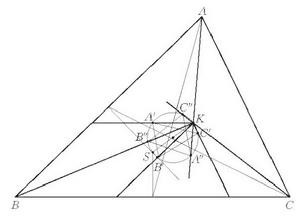
如圖1，從△ABC的外心O0至類似重心K，以OK為直徑作圓，稱為布羅卡爾圓。
從O垂直於原三角形的各邊，作三線，交布羅卡爾圓於A'，B'，C'，那么△A'B'C'稱為 第一布羅卡爾三角形。
從△ABC的各角頂至K，作三線，交布羅卡爾圓於A"，B"，C"，那么△A"B"C"稱為 第二布羅卡爾三角形。
從△ABC的各角頂，平行於△A'B'C'的各邊，作三線，共交於一點S，該點稱為施泰納點。
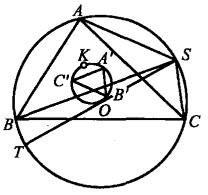圖1相關證明
【例1】三角形的第一布羅卡爾三角形以布羅卡爾圓為外接圓 。
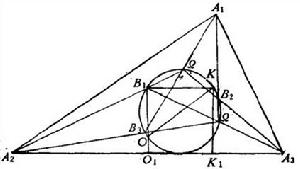圖2
布羅卡爾三角形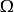
布羅卡爾三角形
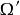布羅卡爾三角形分析 設 中O為外心，K為類似重點， 為正Brocard點， 為負Brocard點， 為第一Brocard三角形，如圖2，為證B在以OK為直徑的圓上，只須證明∠OB₁K=90°。
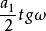布羅卡爾三角形注意到△B₁AA是等腰三角形，底角等於ω，故B₁在AA的垂直平分線OO上，而且BO= 。
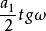布羅卡爾三角形因此，欲證OB₁⊥B₁K，只須證明B₁K//AA，為此，可證明K到AA的距離KK=BO= 。
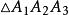布羅卡爾三角形KK₁= KQ₃sinA₁，KQ₃：R=tgω，式中R表 的外接圓半徑，故
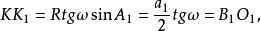布羅卡爾三角形故B₁在OK為直徑的圓上。同理可證B₂，B₃亦在此圓上，即第一Brocard三角形 內接於Brocard圓。
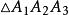布羅卡爾三角形【例2】 與其第一布羅卡爾三角形 有透視關係，即A₁B₁，A₂B₂，A₃B₃共點D。
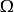布羅卡爾三角形 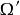布羅卡爾三角形 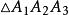布羅卡爾三角形
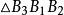布羅卡爾三角形
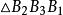布羅卡爾三角形 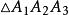布羅卡爾三角形
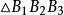布羅卡爾三角形證： 如圖2，A₁B₃，A₂B₁，A₃B₂共點 ，A₁B₂，A₂B₃，A₃B₁共點 ，即 與 有透視關係，又與 有透視關係， 與 亦有透視關係，即A₁B₁，A₂B₂，A₃B₃交於一點D。
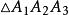布羅卡爾三角形設過A₁，A₂而且切A₃A₁於A₁的圓，與過A₁，A₃而且切A₁A₂於A₁的圓交於點C₁，過A₂, A₃而且切A₁A₂於A₂的圓，與過A₂A₁而且切A₂A₃於A₂的圓交於點C₂，過A₃，A₁而且切A₂ A₃於A₃的圓與過A₃, A₂而且切A₃A₁於A₃的圓交於點C₃，則△C₁C₂C₃叫做 的第二Brocard三角形 。
