簡介
這種濾波器最先由英國工程師斯替芬·巴特沃斯（Stephen Butterworth）在1930年發表在英國《無線電工程》期刊的一篇論文中提出的。
特性
巴特沃斯濾波器的特點是通頻帶內的頻率回響曲線最大限度平坦，沒有起伏，而在阻頻帶則逐漸下降為零。 在振幅的對數對角頻率的波得圖上,從某一邊界角頻率開始,振幅隨著角頻率的增加而逐步減少,趨向負無窮大。
一階巴特沃斯濾波器的衰減率為每倍頻6分貝，每十倍頻20分貝。二階巴特沃斯濾波器的衰減率為每倍頻12分貝、 三階巴特沃斯濾波器的衰減率為每倍頻18分貝、如此類推。巴特沃斯濾波器的振幅對角頻率單調下降，並且也是唯一的無論階數，振幅對角頻率曲線都保持同樣的形狀的濾波器。只不過濾波器階數越高，在阻頻帶振幅衰減速度越快。其他濾波器高階的振幅對角頻率圖和低級數的振幅對角頻率有不同的形狀。
如何用MATLAB構建理想低通濾波器，巴特沃斯低通濾波器，指數低通濾波器和梯形低通濾波器對圖像處理：
i=imread('J20.jpg'); %讀取圖像
I=rgb2gray(i);
I1=imnoise(I,'salt & pepper',0.02);
f=double(I1);
g=fft2(f);
g=fftshift(g);
[N1,N2]=size(g);
n=3; %階次設為3
d0=30; %此處d0為截止頻率
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
h=1/(1+0.414*(d/d0)^(2*n));
result(i,j)=h*g(i,j);
end
end
result=ifftshift(result);
X2=ifft2(result);
J1=uint8(real(X2));
subplot(121),imshow(I1);
title('受高斯噪聲污染的圖像');
subplot(122),imshow(J1);
title('截止頻率為50HZ的巴特沃斯低通濾波處理後');
傳遞函式
巴特沃斯低通濾波器可用如下振幅的平方對頻率的公式表示：
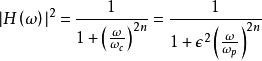巴特沃斯濾波器
巴特沃斯濾波器其中,
= 濾波器的階數
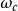巴特沃斯濾波器= 截止頻率 = 振幅下降為 -3分貝時的 頻率
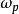巴特沃斯濾波器= 通頻帶邊緣頻率
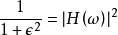巴特沃斯濾波器在通頻帶邊緣的數值
實例
巴特沃斯濾波器
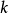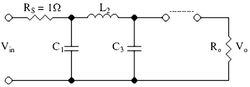
巴特沃斯濾波器階巴特沃斯濾波器的考爾第一型電子線路圖如下: 其中：
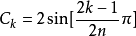巴特沃斯濾波器電容
；
= 奇數
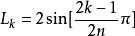巴特沃斯濾波器電感
；
= 偶數
與其它濾波器比較
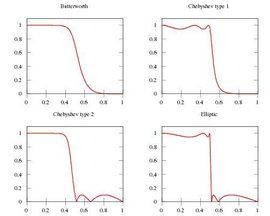
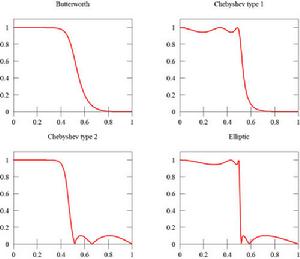
下圖是巴特沃斯濾波器（左上）和同階第一類切比雪夫濾波器（右上）、第二類切比雪夫濾波器（左下）、橢圓函式濾波器（右下）的頻率回響圖。
巴特沃斯濾波器