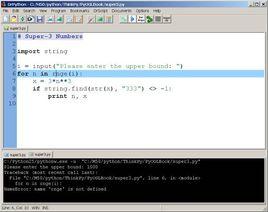
遍歷數組
假設有一堆物品，按 m到 n（含）依次編號。那么這堆物品的總數是多少？我們可能會直覺地認為有( n- m)個物品，但這就和正確答案差了一，犯了 柵欄錯誤。正確答案應該是( n- m+ 1)個物品。
因此，計算機領域中，涉及範圍的時候通常用半開區間來表示，從 m到 n（含）的範圍就表示成從 m到 n+ 1（不含），以避免柵欄錯誤。例如，一個疊代五次的循環可以寫成0到5的半開區間：
循環體首次執行時，i等於0，接著i依次變為1、2、3、4。最後，i會變為5，因此i < 5為假（不成立），循環結束。然而，如果在比較中用的是<=（小於等於），循環體則會執行六次：i依次為0、1、2、3、4、5。同樣，如果i的初值是1而不是0，那么循環體只會執行四次：i依次為1、2、3、4。這些情況都能產生差一錯誤。
還有一種情況就是該用while循環的地方卻用了do-while循環（反之亦然）。Do-while的循環體至少會執行一次。
程式語言間的差異也會產生混淆。從0開始計數是程式語言最為常見的做法，而有些語言中卻以1起始。Pascal語言中可以自定義數組下標的起始值。
柵欄錯誤
柵欄錯誤（有時也稱為 電線桿錯誤或者 燈柱錯誤）是差一錯誤的一種。如以下問題：
建造一條直柵欄（即不圍圈），長30米、每條柵欄柱間相隔3米，需要多少條柵欄柱？
最容易想到的答案10是錯的。這個柵欄有10個間隔，11條柵欄柱。反過來，柱子數給定時，我們也很容易認為間隔數也是這么多。實際上間隔數要比柱子數少一個。
廣義上這個問題可以這么表述： n個電線桿之間有多少個間隔？
如果這一列電線桿不組成一個圈，那么正確答案是 n-1，如果在此前提之下，首尾兩端也計入間隔，那么正確答案是 n+1，如果電線桿圍成一圈，那么答案則是 n。思考之前必須先明確問題的定義，一個情況下的答案可能並不適用於其他情況。柵欄錯誤往往就來源於在數物體還是數間隔的選擇上出了差錯。
除了計算長度，柵欄錯誤還會發生在其他單位中。例如，時間金字塔是一個每10年放置1塊石塊，總共要放置120塊的公共藝術作品，完成這個作品需要花費1190年，而不是1200年。早期的柵欄錯誤也與時間有關，儒略曆最開始計算閏年的方式不正確，導致每三年會有一次閏年（正常情況應該是每四年，即每隔三年）。
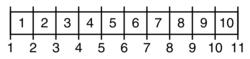n個間隔的直柵欄有n+1條柵欄柱。大數的差一錯誤一般都不會引起大問題。正是在小數字上，尤其是精確度要求很高的時候，差一錯誤可能造成災難。如果負責計算的人員“重蹈覆轍”，差一錯誤甚至可以累積。
安全隱患
不當使用C標準庫中的strncat()函式常常會導致差一錯誤和安全問題。程式設計師經常認為strncat()在寫入字元串結束符時不會超過最大長度。事實上strncat()會在指定的最大長度之後一位元組的位置寫入字元串結束符。如下代碼：
差一錯誤之所以經常在使用C標準庫的時候出現，是因為C標準庫在需不需要減去一位元組這個問題上標準不統一。fgets()和strncpy()這些函式在寫入的時候不會超過最大長度（fgets()會自行把長度減一，只取回(長度 - 1)位元組），而像strncat()這些函式則會越過最大長度。所以程式設計師必須牢記哪些函式需要減去一。
在某些系統上（小端序架構），差一錯誤可導致幀指針的最低位元組被覆蓋，從而使攻擊者能夠劫持調用例程的局部變數，給漏洞攻擊敞開大門。
要避免這類問題，可以使用這些函式的其他改進版本，如strlcat()和strlcpy()，這些改進版在寫入時會考慮緩衝區能容納的大小，因此更加“安全”。（上面代碼的相應部分改成strlcat(buf, s, sizeof(buf))就能解決問題）
