個人簡歷
尼科米迪斯(Nicomedes,約公元前250年前後)希臘數學家。有關尼科米迪斯的生平可從下述事實推斷,他曾批評埃拉托塞尼(Eratosthenes)解決倍立方問題的方法不實用,也不是幾何方法;而阿波羅尼奧斯(Apollonius,(P))指出某一種曲線和蚌線屬同一類型,故此可斷定尼科米迪斯生存年代介人二人之間,約公元前3世紀中期。
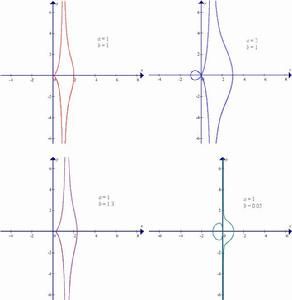
他的主要數學著作是《論蚌線》,可惜已失傳。現只能從帕普斯(Pap-pus,(A))、歐托基奧斯(Eutocius(A))、普羅克洛斯(Proclus)等人的著作中知其內容。尼科米迪斯定義了這樣一種曲線:設OY土OX,直線EF//OX,與OX的距離為a,過O任作直線OAP交EF於A,在此直線上取P,P'點,使AP=AP'=b(定值),則點P與P‘的軌跡為蚌線,O為極點,EF為準線,h為模.曲線分上、下兩支,上支稱為上蚌線,下支稱為下蚌線。此曲線的直角坐標方程為(.}Z+yz)(y一a)z=bzyz;極坐標方程為:一a士b。J111歲蚌線的形狀,取決於a,b的大小,據6>a,b=a,b<a不同的條件,得到不同形狀的蚌線。為了形象地說明蚌線的形成過程,尼科米迪斯還創造了蚌線的機械作圖器,結構簡單,形象直觀。從尼科米迪斯批評埃拉托塞尼的原因可看出,尼科米迪斯研究蚌線是為了實際套用。他以此為工具解決了幾何三大問題中的三等分任意角及倍立方問題。在尼科米迪斯以後千年時間內,對蚌線的研究無多大進展。直到16世紀後期,帕普斯和歐托基奧斯的著作重新引起關注,才再次引發了對蚌線的研究。