簡介
尤登方(Youden square)亦稱尤登設計,
如果從一個拉丁方中划去至少一列(或行)並將行(或列)因子看作區組因子,仍然成為一個平衡不完全區設計的話,則稱這個不完全拉丁方為尤登方,相應的設計稱為尤登方設計。
舉例
(a)五階拉丁方:
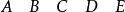 尤登方
尤登方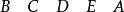 尤登方
尤登方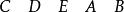 尤登方
尤登方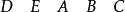 尤登方
尤登方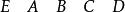 尤登方
尤登方將(a)划去最後一列,得到5×5階尤登方:
 尤登方
尤登方 尤登方
尤登方 尤登方
尤登方 尤登方
尤登方 尤登方
尤登方將(a)划去最後一行,得到4×5階尤登方:
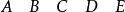 尤登方
尤登方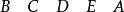 尤登方
尤登方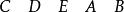 尤登方
尤登方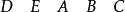 尤登方
尤登方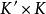 尤登方
尤登方下面兩個是尤登方:
(1)3×4階尤登方:
 尤登方
尤登方 尤登方
尤登方 尤登方
尤登方(2)3×7階尤登方:
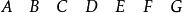 尤登方
尤登方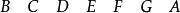 尤登方
尤登方 尤登方
尤登方實際套用
試驗的目的是要考察5種照明度(A、B、C、D、E)對裝配質量的影響。影響裝配質量的因子還有日子(星期1-5)和裝配線(4條)。現採用下列尤登方設計,其中的數據表示裝配的質量。
| \ | 裝配線1 | 裝配線2 | 裝配線3 | 裝配線4 |
| 區組1 | A=3 | B=1 | C=-2 | D=0 |
| 區組2 | B=0 | C=0 | D=-1 | E=7 |
| 區組3 | C=-1 | D=0 | E=5 | A=3 |
| 區組4 | D=-1 | E=6 | A=4 | B=0 |
| 區組5 | E=5 | A=2 | B=1 | C=-1 |
模型
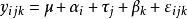 尤登方
尤登方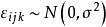 尤登方
尤登方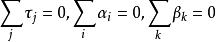 尤登方
尤登方統計分析
將v個處理安排到b個區組中,稱為一個BIBD(b,v,r,k,λ);
1)每個區組包含k個處理——區組大小
2)每個處理在r個區組中出現——處理重複數
3)每對處理在λ個區組中相遇——相遇數
拉丁方
定義
用 r 個拉丁字母排成 r 行 r 列的方陣,使每行每列中每個字母都只能出現一次,這樣的方陣叫r階拉丁方或r×r拉丁方。
表示
如下圖為一個4階或4×4階拉丁方:
 尤登方
尤登方 尤登方
尤登方 尤登方
尤登方 尤登方
尤登方拉丁方設計
分別按拉丁方的字母、行和列安排處理因素和影響因素的試驗設計稱為拉丁方設計。
1.要求條件
(1) 必須是三個因素的試驗,且三個因素的水平數相等;
(2)各因素間無互動作用;
(3)各行、列、字母(處理)間具方差齊性。
2.設計方法
(1)按水平數選基本拉丁方;
(2)隨機排列拉丁方的行、列;
(3)隨機排列處理因素(字母);
(4)確定行、列和字母的因素及其水平。
3.設計特點
(1)同時分別研究三個因素;
(2)設計嚴密,雙向誤差控制;
(3)所需的樣本含量小。
