範疇概念的發展歷程
範疇是從數學的各個領域中概括出來的一個高度抽象的數學系統。對範疇的系統研究起始於S.Eilenberg和S.MacLane在代數拓撲學中的工作,他們在1945年 提出範疇、函子和自然變換等基本概念,其後,在1958年,D.Ken明確地定義並研究了伴隨函子和一般極限理論,在20世紀60、70年代,F.w.Iawvere將範疇方法論引入數學基礎領域,並與M.Tierney等建立了現代Topos理論,極大地推進了範疇理論的研究與套用。
這種理論在提出之後就普遍受到重視而迅速發展起來,並且被套用到數學和理論計算機科學的許多分支中,在數學和理論計算機科學中,範疇理論的概念和方法對於解釋和闡述抽象慨念,確定學科研究架構和建立不同分支之間的關聯等許多方面起著基本的重要作用。
基本知識
定義1 一個 範疇 C由下列內容組成:
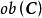 小範疇
小範疇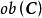 小範疇
小範疇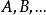 小範疇
小範疇(1) 一個對象類 。 的元稱為 C中的對象,通常用 等表示範疇的對象。
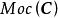 小範疇
小範疇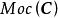 小範疇
小範疇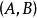 小範疇
小範疇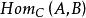 小範疇
小範疇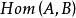 小範疇
小範疇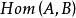 小範疇
小範疇(2) 一個態射類 。 的元稱為 C中的 態射,對於 C中對象的每個有序偶 ,對應有惟一的一個集 ,簡記作 , 中的元稱為 C中以A為 淪域,以B為餘論域的態射。
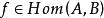 小範疇
小範疇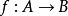 小範疇
小範疇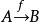 小範疇
小範疇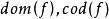 小範疇
小範疇 小範疇
小範疇若 ,則記作 或 有時也用 分別表示 的論域A、餘論域B。
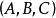 小範疇
小範疇(3) 對於 C中對象的每個有序三元組對應一個稱為 合成(或 複合)的映射
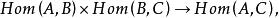 小範疇
小範疇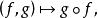 小範疇
小範疇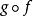 小範疇
小範疇 小範疇
小範疇 小範疇
小範疇稱為和的合成(或複合)。
要求 C中的對象和態射滿足下列公理:
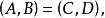 小範疇
小範疇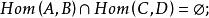 小範疇
小範疇(1)若則
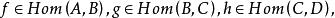 小範疇
小範疇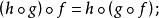 小範疇
小範疇(2)若 則
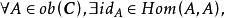 小範疇
小範疇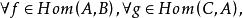 小範疇
小範疇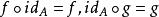 小範疇
小範疇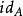 小範疇
小範疇(3)使得有,稱為A上的 恆同態射。
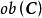 小範疇
小範疇若範疇 C的對象類是集,則稱 C為 小範疇。
相關知識
命題1 若A是範疇C中的對象,則A上的恆同態射是惟一的。
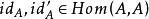 小範疇
小範疇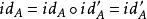 小範疇
小範疇證明: 設都是A上的恆同態射,則由恆同態射的定義,有,這表明A上的恆同態射是惟一的。
定義2設 C與 D都是範疇,若
(1)ob( D)是ob( C)的子類:
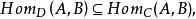 小範疇
小範疇(2)對於 D中的任意對象A和B,有並且 D中態射的合成以及每一對象上的恆同態射都與 C中相同,則稱 D是 C的 子範疇。
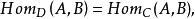 小範疇
小範疇若範疇 D是範疇 C的子範疇,並且對於 D中的任意對象A和B有則稱 D是 C的 滿子範疇。
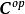 小範疇
小範疇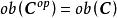 小範疇
小範疇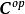 小範疇
小範疇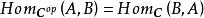 小範疇
小範疇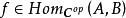 小範疇
小範疇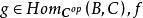 小範疇
小範疇 小範疇
小範疇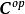 小範疇
小範疇 小範疇
小範疇 小範疇
小範疇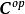 小範疇
小範疇定義3設 C是範疇,則可構造範疇如下:其對象類;對於中的任意對象A和B,態射集並且對於任意和與在中的合成等於與在 C中的合成.範疇稱為範疇 C的 對偶範疇。
對偶範疇的一個重要作用在於它提供了對偶原則。
舉例分析
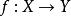 小範疇
小範疇例1 (1) Set:集與映射的範疇,即ob( Set)是全體集構成的類,對於X,Y∈ob( Set),Hom(X,Y)是所有映射構成的集,並且 Set中態射的合成就是映射的合成。
(2) Sp:拓撲空間與連續映射的範疇。
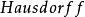 小範疇
小範疇(3) KHausSp:緊空間與連續映射的範疇。
(4) Grp:群與同態的範疇。
(5) O:空範疇。
(6) 設X是集,則可以如下構造一個小範疇,其對象類是集X,並且僅有的態射是恆同映射,稱此範疇為離散(小)範疇。自然,該範疇可以與集等同看待。
例2 集與單射(或滿射或雙射)的範疇是範疇 Set的子範疇,但不是滿子範疇,有限集與映射的範疇是範疇 Set的滿子範疇,範疇 KHausSp是範疇Sp的滿子範疇。

