定義
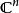 對稱有界域
對稱有界域設 D 為 n 維復歐幾里得空間中的有界域。D 稱為對稱有界域,如果對域 D 中的任一點 P ,存在域D 的全純自同構口,使得
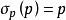 對稱有界域
對稱有界域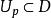 對稱有界域
對稱有界域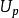 對稱有界域
對稱有界域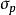 對稱有界域
對稱有界域(1) 以點 p 為孤立不動點,即,又存在點 p 的鄰域,使得在中無其他不動點;
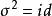 對稱有界域
對稱有界域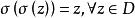 對稱有界域
對稱有界域(2)為恆等映射,即。
發展
E.嘉當證明了對稱有界域為齊性有界域,且在1935 年給出了它們的分類,即證明了對稱有界域為下面一些不可分解的標準對稱有界域的拓撲積,其中標準對稱有界域有四大類,華羅庚稱之為典型域;
另外(並未證明) 至多還有兩個特殊的,一個是復 16 維,另一個是復 27 維。另一方面,他的兒子H.嘉當證明了當n= 1,2,3 時,齊性有界域必為對稱有界域。
因此,E.嘉當提出了下面的著名猜想:齊性有界域必為對稱有界域。這一猜想長期未能解決(為了減弱難度,華羅庚提出了另一猜想:齊性有界域的黎曼曲率必非正)。
嘉當猜想在1959 年由皮亞捷茨基-沙皮羅(Piatetski-Shapiro) 舉出反例予以否定,隨後他引進了西格爾域的概念,證明了齊性有界域必全純等價於齊性西格爾域。進一步的分類問題,至今沒有解決。附加一些條件後,有一些分類結果。

