簡介
多復變數奈望林納函式類是單複變函數論奈望林納函式的推廣。
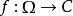多復變數奈望林納函式類
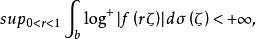多復變數奈望林納函式類設Ω是C 中的有界對稱域，b是它的特徵邊界。如果 在Ω上全純，且滿足 則稱f屬於奈望林納函式類，記為N(Ω)。
有界對稱域
有界對稱域是一類特殊的復有界域。若有界域D中每點二均為D的一個對合全純微分同胚的孤立不動點，則稱D為有界對稱域。
有界對稱域對其上的伯格曼度量是非緊型的埃爾米特對稱空間。反之，一個非緊型埃爾米特對稱空間一定全純微分同胚於一個有界對稱域。以有界對稱域表示非緊型埃爾米特對稱空間，稱為後者的哈瑞斯-祥德拉實現。
複變函數論
複變函數論產生於十八世紀。1774年，歐拉在他的一篇論文中考慮了由複變函數的積分導出的兩個方程。而比他更早時，法國數學家達朗貝爾在他的關於流體力學的論文中，就已經得到了它們。因此，後來人們提到這兩個方程，把它們叫做“達朗貝爾-歐拉方程”。到了十九世紀，上述兩個方程在柯西和黎曼研究流體力學時，作了更詳細的研究，所以這兩個方程也被叫做“柯西-黎曼條件”。
複變函數論的全面發展是在十九世紀，就像微積分的直接擴展統治了十八世紀的數學那樣，複變函數這個新的分支統治了十九世紀的數學。當時的數學家公認複變函數論是最豐饒的數學分支，並且稱為這個世紀的數學享受，也有人稱讚它是抽象科學中最和諧的理論之一。
