概述
每個線性規劃問題都有一個與之對應的對偶問題。對偶問題是以原問題的約束條件和目標函式為基礎構造而來的。對偶問題也是一個線性規劃問題，因此可以採用單純形法求解。對偶問題的最優解也可以通過原問題的最優解得到，反之亦然。而且，在某些情況下，利用對偶理論求解線性規劃問題更為簡單，而且有助於深入了解待求問題的本質。
對偶線性規劃的經濟背景是：若原問題是利用有限資源安排最優生產方案，以獲得最大總產值的線性規劃問題，則它的對偶問題就是在相同資源的條件下，正確估計資源的使用價值，以達到支付最少費用的線性規劃問題.簡言之，若原問題為求解資源的最優配置問題，則對偶問題就是求解估價資源的使用價值問題。
基本性質
原始線性規劃與對偶線性規劃問題不僅在數學模型的形式上存在著相互對應的關係，而且它們的目標函式、可行解及最優解之間也存在著確定的聯繫。
設有一對線性規劃問題為：
（1）原始問題
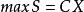對偶線性規劃求
滿足
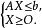對偶線性規劃（2）對偶問題
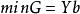對偶線性規劃求
滿足
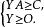對偶線性規劃定理：互為對偶的線性規劃（1）和（2）有最優解的充分必要條件是它們同時有可行解。
證明：必要性是顯然的，下面來證明充分性。
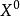對偶線性規劃
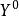對偶線性規劃設是（1）的可行解，是（2）的可行解。
則有
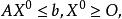對偶線性規劃
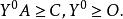對偶線性規劃
對偶線性規劃若是（1）的任意一個可行解，則有
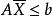對偶線性規劃 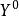對偶線性規劃 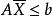對偶線性規劃成立。用左乘式子，得
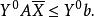對偶線性規劃 對偶線性規劃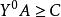
對偶線性規劃用右乘不等式的兩邊，得
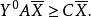對偶線性規劃
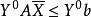對偶線性規劃
對偶線性規劃由和兩個式子，得
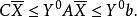對偶線性規劃
對偶線性規劃上式說明原始問題（1）的目標函式在可行解集合上有上界，所以（1）有最優解。
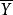對偶線性規劃設是（2）的任意一個可行解，用同樣的推理方法可得
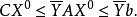對偶線性規劃
對偶線性規劃上式表示對偶問題（2）的目標函式在可行解集合上有下界，所以（2）有最優解。證明完畢。
