概念
1954年美國數學家C.萊姆基提出對偶單純形算法(Dual Simplex Method)。單純形法是從原始問題的一個可行解通過疊代轉到另一個可行解，直到檢驗數滿足最優性條件為止。
對偶單純形法則是從滿足對偶可行性條件出發通過疊代逐步搜尋原始問題的最優解。在疊代過程中始終保持基解的對偶可行性，而使不可行性逐步消失。
設原始問題為min{cx|Ax=b，x≥0}，則其對偶問題（Dual Problem）為 max{yb|yA≤c}。當原始問題的一個基解滿足最優性條件時,其檢驗數cBB-1A-c≤0。即知y=cBB-1（稱為單純形運算元）為對偶問題的可行解。所謂滿足對偶可行性，即指其檢驗數滿足最優性條件。因此在保持對偶可行性的前提下，一當基解成為可行解時，便也就是最優解。
對偶單純形算法（dual simplex method）是純形方法的一種對稱變形．對於原單純形方法而言，在疊代過程中始終保持相應的解對原問題是可行的，並不斷改善對偶問題解（即判別係數）的可行性，直至可行．而對偶單純形方法則是始終保持對偶問題的解的可行性，並不斷改善原問題解的可行性，直至滿足原問題。
基本原理
所謂滿足對偶可行性，即指其檢驗數滿足最優性條件。只要保持檢驗數滿足最優性條件前提下，一旦基解成為可行解時，對偶問題和原問題均可行，由強對偶性證明，二者均有最優解。
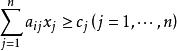對偶單純形算法
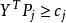對偶單純形算法設原始問題的標準形式為max{cx|Ax=b，x≥0}，則其對偶問題(Dual Problem)為 min{y|y≤c}。當原問題的一個基解滿足最優性條件時，其檢驗數小於等於0，當σ=c-z=c-CBA≤0時，既有 或 ，即知單純形運算元y=CB為對偶問題的可行解。換而言之，只要保證檢驗數σ≤0，則對偶問題一定存在可行基B。
在初始單純形表中，一般此可行基B都為單位矩陣I，這時候只要能夠保持檢驗數持續小於等於0疊代下去，通過變換到一個相鄰的目標函式值較小的基可行解（因為對偶問題是求目標函式極小化），並循環進行，一到X=Bb≥0時，原問題也為可行解。這時，對偶問題和原問題均為可行解，而且兩者的可行解就是最優解，這就是對偶單純形法求解線性規劃的基本思路。
一旦最終基變數X≥0，原問題也滿足最優解條件的原因是：對偶問題的最終單純形表中的基變數X=Bb和原問題的最終單純形表中的檢驗數的相反數CB取值相等，不難觀察到原問題的檢驗數σ=c-z-CB=-Bb≤0，其檢驗數滿足最優性條件。（註：這裡的B並不是同一個矩陣，它們是各自問題的初始可行基，但C和b在本質上是同一個向量。）
雖然，本方法借鑑了對偶理論的思路，但是它是求解原問題而非對偶問題的一個方法。而且，一般用對偶單純形法解決的是原始問題是極小化問題，min{cx|Ax=b，x≥0}，但是只要先標準化為max{cx|Ax=b，x≥0}即於上面一致。
