基本思想
原始-對偶方法是求解線性規劃的一種算法,指求解線性規劃的一類特殊對偶型方法,其特殊性在於,它是以鬆弛互補性條件為基礎去構造一個由原問題產生的限定問題,並通過求解此限定問題去改善解對原問題的可行性,這一過程含有單純形法與對偶單純形方法的思想,所以有此名 。
方法步驟
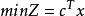 原始-對偶方法
原始-對偶方法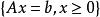 原始-對偶方法
原始-對偶方法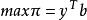 原始-對偶方法
原始-對偶方法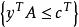 原始-對偶方法
原始-對偶方法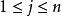 原始-對偶方法
原始-對偶方法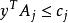 原始-對偶方法
原始-對偶方法設原問題(P)為,滿足;其對偶問題(D)為,滿足,已知y是(D)的一個可行解,即對於,均有,A為A的第j列,其方法為:
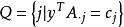 原始-對偶方法
原始-對偶方法1.由已知y,記,求解限定問題(RP):
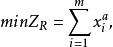 原始-對偶方法
原始-對偶方法滿足
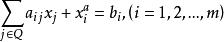 原始-對偶方法
原始-對偶方法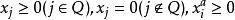 原始-對偶方法
原始-對偶方法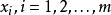 原始-對偶方法
原始-對偶方法及(為人造變數)。
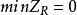 原始-對偶方法
原始-對偶方法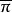 原始-對偶方法
原始-對偶方法2.(最優判定) 是否? 若是,停止疊代,則當前解為最優解,否則,記為限定問題(RP)的對偶問題的最優解。
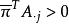 原始-對偶方法
原始-對偶方法3.檢驗是否存在?若不存在,則停止疊代,原問題不可行。
4.(調整指標集Q及對偶解y)取
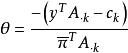 原始-對偶方法
原始-對偶方法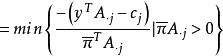 原始-對偶方法
原始-對偶方法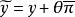 原始-對偶方法
原始-對偶方法並以作為新的對偶解,轉至第1步。
對於某些組合最佳化問題,如最短路問題等,相應的限定問題(RP)具有特定的簡捷和直觀的形式,給求解(RP)帶來方便,因此,原始-對偶方法常常加以套用 。

