內容簡介
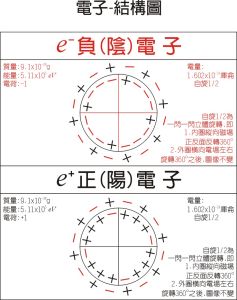電子-內部結構模型圖Franck-Condonprinciple解釋分子電子光譜帶振動結構（見雙原子分子電光譜帶）強度分布的基本原理。主要內容是分子中的子躍遷遠比分子振動迅速，電子躍遷後的一瞬間，分內原子核的相對距離和速度幾乎與躍遷前完全一樣。個思想是J.夫蘭克在1925年首先提出來的，1928年E.U.康登運用波動力學，使它進一步完善。
對於吸收光譜，因為大多數分子的電子和下振動態原來都處於基態，即勢能曲線的最低點忽略零點振動。根據夫蘭克-康登原理，電子躍遷後的一瞬間,分子將處於A點正上方上勢能曲線上的B點處。B點處分子核心間距離和A點處的相同,並且相對速度為零（勢能曲線上各點的振動動能為零）。根據兩勢能曲線的最低點核距r值的對比,可以解釋吸收光譜電子帶強度分布的不同情況。此原理套用於發射光譜，要考慮到分子振動時，在反轉點分子停留的時間最長，電子躍遷發生在這兩點附近的幾率最大。若電子躍遷發生於躍遷後的一瞬間分子將處於A點正下方的C點；若躍遷發生於B點，則躍遷後分子將處於D點。因此，對於一定的上振動量子數v′，有兩個下振動量子數v″不同的電子帶強度最大。將各v′-v″帶的相對強度按圖3的方式排列，各強度最大的帶將構成一拋物線，稱為康登拋物線。
富蘭克-康登原理的經典說法是，在發生電子躍遷時，分子中各原子核的位置及其環境可視為幾乎不變。所形成的狀態稱為弗蘭克-康登態，躍遷方式屬於垂直躍遷。這些躍遷發生在核動能最小的點上，也就是在振動的極限位置上，因此躍遷時核間距或動量都沒有明顯的變化。此原理的量子力學表述為：振動躍遷的強度之和與此躍遷的始態及終態相應的兩個振動波函式的重疊積分的平方成反比。
富蘭克—康登原理：富蘭克首先提出這一原理的基本思想(1925)，康登用量子力學加以說明(1928)。他們認為：電子躍遷的過程是一個非常迅速的過程，躍遷後電子態雖有改變，但核的運動在這樣短的時周內來不及跟上，保持著原狀(原來的核間距和振動速度)。 由於電子和原於核質量的顯著差別，電子的運動速度比原子核快得多，以至電子在躍遷過程中原子核間距離基本保持不變．這表示在兩個不同電子態的勢能曲線之間，要用垂線來表示電子躍遷過程．這個原理就稱為Franck-Condon原理，它成功地朗釋了零譜帶系的強度分布。
