寄生調幅

寄生調幅是指調頻波通過RLC迴路產生調幅波的現象。寬頻帶調頻波中包含不同頻率的信號分量（頻率連續分布）。當通過RLC迴路時，RLC迴路對不同頻率分量顯現出不同的輸出阻抗，從而導致輸出信號幅度變化，成為調幅波形式。

寄生調幅產生的原因

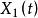寄生調幅

為了討論寄生調幅問題，我們選用如圖1所示的典型採集系統，假定系統輸入信號 為單一頻率的正弦波，系統增益為1。

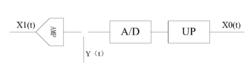圖1 典型的採集系統框圖

設:

寄生調幅

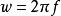寄生調幅

寄生調幅

其中， 。當採樣信號頻率與被採樣信號頻率成整數倍關係時，對被採樣信號來說，每個周期的採樣點個數是一樣的，對應點的相位是不變的。因此, 採樣所得信號的幅值是一個穩定的值。

寄生調幅

當採樣信號頻率大於被採樣信號頻率兩倍時，輸出信號不會產生假頻，採樣輸出信號頻率與被採樣信號頻率相等。

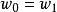寄生調幅

但由於採樣效應的存在, 採樣輸出信號的幅值的隨機性所決定的。採樣後信號幅度誤差的機率分一般總是小於被採樣信號的幅值。

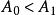寄生調幅

這是由於採樣信號與被採樣信號之間初始相位的隨機性所決定的。採樣後信號幅度誤差的機率分布如表1所示。

表1 採樣後信號幅值誤差機率分布表

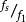寄生調幅	最大採樣誤差(%)	採樣誤差機率分布(P)		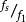寄生調幅	最大採樣誤差(%)	採樣誤差機率分布(P)
		>5%	<5%			>5%	5~4%	4~3%	3~2%	2~1%	<1%
				10	4.84	0	0.07	0.13	0.14	0.15	0.51
2	100.00	0.82	0.18	20	1.21	0	0	0	0	0.11	0.89
3	49.72	0.78	0.22	30	0.54	0	0	0	0	0	1
4	29.17	0.69	0.31	40	0.30	0	0	0	0	0	1
5	18.13	0.48	0.52	50	0.20	0	0	0	0	0	1
6	13.00	0.37	0.63	60	0.13	0	0	0	0	0	1
7	9.81	0.31	0.69	70	0.10	0	0	0	0	0	1
8	7.56	0.29	0.71	80	0.07	0	0	0	0	0	1
9	0.98	0.11	0.89	90	0.06	0	0	0	0	0	1
10	4.84	0	1	100	0.05	0	0	0	0	0	1

寄生調幅

寄生調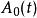幅

寄生調幅

當採樣信號頻率與被採樣信號頻率不成整數倍關係時, 對被採樣信號來說, 每個周期內的採樣點數可能是不一樣的, 其對應點的相位是不同的。因此,採樣輸出信號幅值是隨時間呈周期性變化的, 而不再是一個穩定的值 ，其中 的最大值等於被採樣信號得幅值，即 .

圖2 寄生調幅波產生原因示意圖

這種由於採樣產生的信號幅值的變化, 是我們所不期望的, 這種信號幅值變化是寄生在採樣過程中的。又由於採樣信號頻率與被採樣信號頻率不成整數倍關係, 其採樣輸出信號的幅值變化與調幅波有些類似, 因此, 我們稱這種幅度變化為 寄生調幅。

當採樣信號頻率與被採樣信號頻率不成整數倍關係時, 對被採樣信號每個周期的採樣點相位是不一樣的, 這可以從圖2 中直觀地看出。

寄生調幅波形特點

圖3 給出了實測的幾種典型寄生調幅波形圖。

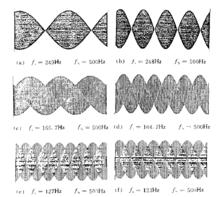圖3 實測典型寄生調幅波形圖

從圖3 中可以直觀地看出, 當採樣信號頻率與被採樣信號頻率不成整數倍關係時, 其產生的寄生調幅波有如下特點:

1、寄生調幅波的包絡線類似於整流正弦波;

2、當採樣信號頻率與被採樣信號頻率接近偶數倍時, 寄生調幅波是正負對稱的( 這是由於對採樣信號正負半周採樣個數相等造成的) ;

3、當採樣信號頻率與被採樣信號頻率接近奇數倍時, 寄生調幅波幅波振幅正負是不對稱的(這是由於對被採樣信號正負半周採樣個數不同造成的) ;

4、當採樣信號頻率與被採樣信號頻率之比越大時, 寄生調幅幅度越小, 反之亦然( 這與表1 的計算結果是一致的)。

寄生調幅的調製度與寄生調幅頻率的計算

寄生調幅調製度的計算

寄生調幅

若將寄生調幅的調製度 定義為:

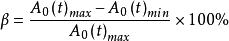寄生調幅

寄生調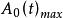幅

寄生調幅

式中， 為採樣輸出最大幅值； 為採樣輸出最小幅值。

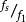寄生調幅

寄生調幅的調製度是 的函式。表l 中最大採樣誤差即為寄生調幅的調製度。

寄生調幅波包絡線頻率的計算

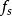寄生調幅

在實際設計數位化信號採集系統時, 採樣信號頻率fs 至少大於兩倍的被採樣信號頻率( ), 即

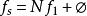寄生調幅

寄生調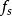幅

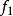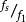寄生調幅

寄生調幅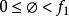

寄生調幅

寄生調幅

式中， 為採樣信號頻率， 為被採樣信號頻率，N為正整數（N>=2）, 為 的餘數，且 .

寄生調幅波的調製頻率可由下式確定:

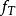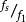寄生調幅

寄生調幅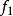

寄生調幅

寄生調幅

寄生調幅

寄生調幅

其中， 為寄生調幅波包絡線頻率； 為 的餘數；為被採樣信號頻率；上式表明, 當等於零時, 寄生調幅波包絡線頻率為零, 即沒有寄生調幅現象產生。當不等於零時, 即不成整數倍關係時, 則會產生寄生調幅現象。