由來
學生 t檢驗是威廉·戈塞為了觀測釀酒品質於1908年所提出的,“學生”則是他的筆名。基於克勞德·健力士(Claude Guinness)聘用從牛津大學 和劍橋大學出來的最好的畢業生,以將生物化學及統計學套用到健力士工業流程的創新政策,戈斯特受僱於都柏林的健力士釀酒廠擔任統計學家。戈斯特提出了 t檢驗以降低啤酒質量監控的成本。戈斯特於1908年在《Biometrika》期刊上公布t檢驗,但因其老闆認為其為商業機密而被迫使用筆名,統計學論文內容也跟釀酒無關。實際上,其他統計學家是知道戈斯特真實身份的。
今日,它更常被套用於小樣本判斷的置信度。
套用
最常用t檢驗的情況有:
•單樣本檢驗:檢驗一個常態分配的總體的均值是否在滿足零假設的值之內,例如檢驗一群軍校男生的身高的平均是否符合全國標準的170公分界線。
•雙樣本檢驗:其零假設為兩個常態分配的總體的均值之差為某實數,例如檢驗二群人的身高之平均是否相等。這一檢驗通常被稱為學生t檢驗。但更為嚴格地說,只有兩個總體的方差是相等的情況下,才稱為學生t檢驗;否則,有時被稱為Welch檢驗。以上談到的檢驗一般被稱作“未配對”或“獨立樣本”t檢驗,我們特別是在兩個被檢驗的樣本沒有重疊部分時用到這種檢驗方式。
•“配對”或者“重複測量”t檢驗:檢驗同一統計量的兩次測量值之間的差異是否為零。舉例來說,我們測量一位病人接受治療前和治療後的腫瘤尺寸大小。如果治療是有效的,我們可以推定多數病人接受治療後,腫瘤尺寸應該是變小了。
•檢驗一條回歸線的斜率是否顯著不為零。
前提假設
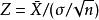 學生t檢驗
學生t檢驗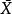 學生t檢驗
學生t檢驗 學生t檢驗
學生t檢驗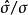 學生t檢驗
學生t檢驗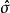 學生t檢驗
學生t檢驗大多數的 t檢定之統計量具有 t= Z/ k的形式,其中 Z與 k是已知資料的函式。 Z通常被設計成對於對立假說有關的形式,而 k是一個尺度參數使 t服從於 t分布。以單樣本 t檢驗為例,其中為樣本平均數,n為樣本數,為總體標準差。至於 k在單樣本 t檢驗中為,其中為樣本的標準偏差。在符合零假說的條件下, t檢定有以下前題:
•Z服從標準常態分配
•(n-1)k服從自由度(n-1)的卡方分布
•Z與k互相獨立
單樣本t檢驗
檢驗零假說為一群來自正態分配獨立樣本 x之母體期望值 μ為 μ可利用以下統計量
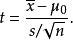 學生t檢驗
學生t檢驗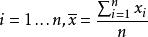 學生t檢驗
學生t檢驗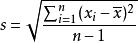 學生t檢驗
學生t檢驗其中為樣本平均數,為樣本標準偏差, n為樣本數。該統計量 t在零假說: μ= μ為真的條件下服從自由度為 n−1的t分布。
配對樣本t檢驗
配對樣本 t檢驗可視為單樣本 t檢驗的擴展,不過檢驗的對象由一群來自正態分配獨立樣本更改為二群配對樣本之觀測值之差。
若二群配對樣本 x與 x之差為 d= x− x獨立且來自正態分配,則 d之母體期望值 μ是否為 μ可利用以下統計量
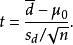 學生t檢驗
學生t檢驗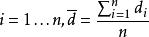 學生t檢驗
學生t檢驗 學生t檢驗
學生t檢驗其中為配對樣本差值之平均數,為配對樣本差值之標準偏差, n為配對樣本數。該統計量 t在零假說: μ= μ為真的條件下服從自由度為 n−1的t分布。
獨立雙樣本t檢驗
樣本數及方差相等
若二群獨立樣本 x與 x具有相同之樣本數 n,並且彼此獨立及來自二個方差相等的正態分配,則二群母體之期望值差 μ- μ是否為 μ可利用以下統計量
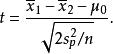 學生t檢驗
學生t檢驗該統計量 t在零假說: μ- μ= μ為真的條件下服從自由度為2 n−2的t分布。
樣本數不相等但方差相等
若二群獨立樣本 x與 x具有不相同之樣本數 n與 n,並且彼此獨立及來自二個方差相等的正態分配,則二群母體之期望值之差 μ- μ是否為 μ可利用以下統計量
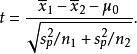 學生t檢驗
學生t檢驗該統計量 t在零假說: μ- μ= μ為真的條件下服從自由度為 n+ n−2的t分布。
樣 本數及方差皆不相等
若二群獨立樣本 x與 x具有相等或不相同之樣本數 n與 n,並且彼此獨立及來自二個方差不相等的正態分配,則二群母體之期望值之差 μ- μ是否為 μ可利用以下統計量
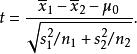 學生t檢驗
學生t檢驗該統計量 t在零假說: μ- μ= μ為真的條件下服從自由度為
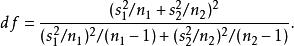 學生t檢驗
學生t檢驗之t分布。這種方法又常稱為Welch檢驗。
電腦軟體
大多數的試算表軟體及統計軟體,諸如QtiPlot、OpenOffice.org Calc、LibreOffice Calc、Microsoft Excel、SAS、SPSS、Stata、DAP、gretl、R、Python、PSPP、Minitab等,都可以進行 t檢驗之運算。
另請參閱
方差齊性檢驗(F檢驗)
