存在量詞

短語有些、至少有一個、有一個、存在等都有表示個別或一部分的含義，這樣的詞叫作存在量詞。含有存在量詞的命題叫作特稱命題。其形式為有的S是P。特稱命題使用存在量詞，如有些、很少等，也可以用基本上、一般、只是有些等。含有存在性量詞的命題也稱存在性命題。短語存在一個、至少一個在邏輯中通常叫做存在量詞，用符號∃表示。含有存在量詞的命題，叫做特稱命題（存在性命題）。

基本信息

• 中文名：存在量詞
• 英文名：existential quantifier

• 定義：表示個別或一部分的含義
• 特稱命題：含有存在量詞的命題
• 形式：有的S是P

舉例說明

存在量詞

（1）有一個素數不是奇數；
（2）有的平行四邊形是菱形。
常見的存在量詞還有“有些”、“有一個”、“對某個”、“有的”等。
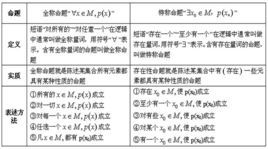
特稱命題“存在M中的一個x，使p（x）成立”。簡記為：∃x∈M，p（x）。
讀作：存在一個x屬於M，使p（x）成立。

“所有烏鴉都是黑的。”這是一個全稱命題，有了這個前提我們就能夠推出：“有些烏鴉是黑的。”但反過來，從“有些烏鴉是黑的”推出“所有烏鴉都是黑的”就是錯的。簡言之，全稱到特稱是合乎邏輯的演繹，但特稱到全稱你就得當心。
以“北半球的烏鴉都是黑的”和“南半球的烏鴉都是黑的”兩個特稱判斷為前提，可以推出“所有烏鴉都是黑的”這個全稱命題必然為真。這就是一種前提里有特稱命題的推理。但不一定非得這樣，當“天下烏鴉一般黑”這個命題為真時，“所有烏鴉都是黑的”也必然為真，這也就是結論全稱、前提同樣全稱的情況（形式邏輯中有一個“同一律”）。除此之外，還可以由一組單稱判斷推導出一個主項為有限外延的全稱判斷。綜合起來，共有三種情況，前提可能是全稱判斷、特稱判斷或單稱判斷三種，所以就不一定是特稱判斷。

主要區別

在語句中含有短語“所有”、“每一個”、“任何一個”、“任意一個”、“一切”等都是在指定範圍內，表示整體或全部的含義，這樣的詞叫作全稱量詞。
含有全稱量詞的命題叫作全稱命題。
全稱量詞的否定是存在量詞。