簡介
奇異分布是一種機率分布，又稱退化分布，和離散分布、連續分布一起構成機率分布的三種基本類型。
奇異分布在一個勒貝格測度為零的區域上有正的分布密度，但是在任何單點上的分布機率也為零，同時由於其支撐集測度為零，所以也沒有密度函式，因此奇異分布既不是離散分布（在單點上有正的機率），也不是連續分布（在一塊勒貝格測度不為零的區域上有正的分布密度）。
奇異分布的典型代表為康托分布。
判定
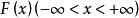奇異分布奇異分布是一類理論上很有價值的機率分布函式，實際套用中也經常遇到。如果分布函式 F(x) 連續，但它的導函式幾乎處處（關於勒貝格測度而言）等於0，則稱分布函式為奇異型的。
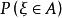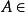奇異分布
奇異分布如果隨機變數 ξ 的分布函式是奇異型的，則稱該隨機變數及其機率分布（ ）為奇異型的。
勒貝格測度
勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析，特別是用於定義勒貝格積分。
可以賦予一個體積的集合被稱為勒貝格可測；勒貝格可測集A 的體積或者說測度記作 λ(A) 。一個值為 ∞ 的勒貝格測度是可能的，但是即使如此，在假設選擇公理成立時， R 的所有子集也不都是勒貝格可測的。不可測集的“奇特”行為導致了巴拿赫-塔斯基悖論這樣的命題，它是選擇公理的一個結果。
