介紹信息
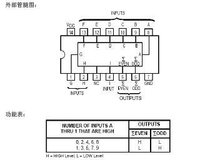 奇偶校驗
奇偶校驗與一段信息關聯的冗餘信息。在WindowsNTServer中,帶奇偶校驗的帶區集意味著每行有一個附加的奇偶校驗帶區。因此,必須使用至少三個(而不是兩個)磁碟才能考慮該附加的奇偶校驗信息。奇偶校驗帶區包含該帶區內數據的XOR(稱為"排它性“或”的布爾操作")。重新生成失敗的磁碟時,WindowsNTServer將使用這些帶區中與完好磁碟上數據關聯的奇偶校驗信息重新在失敗盤上創建數據。請參閱容錯;帶區集;帶奇偶校驗的帶區集
奇偶校驗能夠檢測出信息傳輸過程中的部分誤碼(1位誤碼能檢出,2位及2位以上誤碼不能檢出),同時,它不能糾錯。在發現錯誤後,只能要求重發。但由於其實現簡單,仍得到了廣泛使用。
為了能檢測和糾正記憶體軟錯誤,首先出現的是記憶體“奇偶校驗”。記憶體中最小的單位是比特,也稱為“位”,位只有兩種狀態分別以1和0來標示,每8個連續的比特叫做一個位元組(byte)。不帶奇偶校驗的記憶體每個位元組只有8位,如果其某一位存儲了錯誤的值,就會導致其存儲的相應數據發生變化,進而導致應用程式發生錯誤。而奇偶校驗就是在每一位元組(8位)之外又增加了一位作為錯誤檢測位。在某位元組中存儲數據之後,在其8個位上存儲的數據是固定的,因為位只能有兩種狀態1或0,假設存儲的數據用位標示為1、1、1、0、0、1、0、1,那么把每個位相加(1+1+1+0+0+1+0+1=5),結果是奇數。對於偶校驗,校驗位就定義為1,反之則為0;對於奇校驗,則相反。當CPU讀取存儲的數據時,它會再次把前8位中存儲的數據相加,計算結果是否與校驗位相一致。從而一定程度上能檢測出記憶體錯誤,奇偶校驗只能檢測出錯誤而無法對其進行修正,同時雖然雙位同時發生錯誤的機率相當低,但奇偶校驗卻無法檢測出雙位錯誤。
監督碼率
奇偶監督碼是一種增加二進制傳輸系統最小距離的簡單和廣泛採用的方法。例如,單個的奇偶監督將使碼的最小距離由一增加到二。
一個二進碼字,如果它的碼元有奇數個1,就稱為具有奇性。例如,碼字“1011010111”有七個1,因此,這個碼字具有奇性。同樣,偶性碼字具有偶數個1。注意奇性檢測等效於所有碼元的模二加,並能夠由所有碼元的異或運算來確定。對於一個n位字,奇性由式(8-1)給出:
奇性=a0⊕a1⊕a2⊕…⊕an(8-1)
很明顯,用同樣的方式,我們也能夠根據每一個碼字的零的個數來構成奇偶監督。
單個的奇偶監督碼可描述為:給每一個碼字加一個監督位,用它來構成奇性或偶性監督。例如,在圖8-2中,對於二進碼就是這樣做的。可以看出,附加碼元d2,是簡單地選來使每個字成為偶性的。因此,若有一個碼元是錯的,就可以分辨得出,因為奇偶監督將成為奇性。
在一個典型系統里,在傳輸以前,由奇偶發生器把奇偶監督位加到每個字中。原有信息中的數字在接收機中被檢測,如果沒有出現正確的奇、偶性,這個信息標定為錯誤的,這個系統將把錯誤的字拋掉或者請求重發。注意,用單個的奇偶監督碼僅能檢出奇數個碼元的錯誤。
例如考慮圖8-4里的奇性監督碼。把奇、偶監督位加到一個8-4-2-1BCD碼,使之能夠進行奇監督(將所有監督位反過來將產生偶監督碼)。可以看到,如果將任何碼字里的奇數個碼元反過來,那么將成為偶性碼,因而,無效的字是可以分辨出來的。然而,如果有兩個或四個碼元反過來,那末奇偶監督將仍然是奇性碼,並且這個字被認為是正確的。只當一個給定的字里同時出現兩個錯誤的機率被忽略不計時,單個的奇偶監督才是有效的,實際上,奇監督碼比偶監督碼可取,因為它排除了傳輸全0的情況。
單向校驗
概述
單向奇偶校驗(Row Parity)由於一次只採用單個校驗位,因此又稱為單個位奇偶校驗(Single Bit Parity)。傳送器在數據禎每個字元的信號位後添一個奇偶校驗位,接收器對該奇偶校驗位進行檢查。典型的例子是面向ASCII碼的數據信號禎的傳輸,由於ASCII碼是七位碼,因此用第八個位碼作為奇偶校驗位。
單向奇偶校驗又分為奇校驗(Odd Parity)和偶校驗(Even Parity),傳送器通過校驗位對所傳輸信號值的校驗方法如下:奇校驗保證所傳輸每個字元的8個位中1的總數為奇數;偶校驗則保證每個字元的8個位中1的總數為偶數。
顯然,如果被傳輸字元的7個信號位中同時有奇數個(例如1、3、5、7)位出現錯誤,均可以被檢測出來;但如果同時有偶數個(例如2、4、6)位出現錯誤,單向奇偶校驗是檢查不出來的。
一般在同步傳輸方式中常採用奇校驗,而在異步傳輸方式中常採用偶校驗。
校驗方法
奇校驗:就是讓原有數據序列中(包括你要加上的一位)1的個數為奇數
1000110(0)你必須添0這樣原來有3個1已經是奇數了所以你添上0之後1的個數還是奇數個。
偶校驗:就是讓原有數據序列中(包括你要加上的一位)1的個數為偶數
1000110(1)你就必須加1了這樣原來有3個1要想1的個數為偶數就只能添1了。
雙向校驗
為了提高奇偶校驗的檢錯能力,可採用雙向奇偶校驗(Row and Column Parity),也可稱為雙向冗餘校驗(Vertical and Longitudinal Redundancy Checks)。
雙向奇偶校驗,又稱“方塊校驗”或“垂直水平”校驗。
例:
1010101×
1010111×
1110100×
0101110×
1101001×
0011010×
×××××××
“×”表示 奇偶校驗所採用的奇校驗或偶校驗的校驗碼。
如此,對於每個數的關注就由以前的1×7次增加到了7×7次。因此,比單項校驗的校驗能力更強。
簡單的校驗數據的正確性,在計算機里都是010101二進制表示,每個位元組有八位二進制,最後一位為校驗碼,奇校驗測算前七位里1的個數合的奇偶性,偶校驗測算前七位里0的個數的奇偶性。當數據里其中一位變了,得到的奇偶性就變了,接收數據方就會要求傳送方重新傳數據。奇偶校驗只可以簡單判斷數據的正確性,從原理上可看出當一位出錯,可以準確判斷,如同時兩個1變成兩個0就校驗不出來了,只是兩位或更多位及校驗碼在傳輸過程中出錯的機率比較低,奇偶校驗可以用的要求比較低的套用下。
範例信息
串列數據在傳輸過程中,由於干擾可能引起信息的出錯,例如,傳輸字元‘E’,其各位為:
0100,0101=45H
D7 D0
由於干擾,可能使位變為1,(為什麼不變0?)這種情況,我們稱為出現了“誤碼”。我們把如何發現傳輸中的錯誤,叫“檢錯”。發現錯誤後,如何消除錯誤,叫“糾錯”。最簡單的檢錯方法是“奇偶校驗”,即在傳送字元的各位之外,再傳送1位奇/偶校驗位。可採用奇校驗或偶校驗。
奇校驗:所有傳送的數位(含字元的各數位和校驗位)中,“1”的個數為奇數,如:
1 0110,0101
0 0110,0101
偶校驗:所有傳送的數位(含字元的各數位和校驗位)中,“1”的個數為偶數,如:
1 0100,0101
0 0100,0101
奇偶校驗能夠檢測出信息傳輸過程中的部分誤碼(1位誤碼能檢出,2位及2位以上誤碼不能檢出),同時,它不能糾錯。在發現錯誤後,只能要求重發。但由於其實現簡單,仍得到了廣泛使用。有些檢錯方法,具有自動糾錯能力。如循環冗餘碼(CRC)檢錯等。