簡介
計算複雜度理論中, 多項式譜系是一個複雜度系列。它從P、NP和反NP複雜度類逐級產生至預言機。它類似於數理邏輯中算數階層和分析階層,只不過是由逐級放寬資源限制而產生的。
定義
多項式譜系有數個等價的定義。
(1)用預言機定義多項式譜系。首先定義
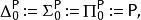 多項式譜系
多項式譜系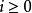 多項式譜系
多項式譜系其中P是能在多項式時間內解決的決定性問題。然後對所有 定義
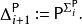 多項式譜系
多項式譜系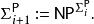 多項式譜系
多項式譜系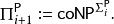 多項式譜系
多項式譜系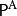 多項式譜系
多項式譜系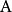 多項式譜系
多項式譜系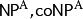 多項式譜系
多項式譜系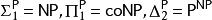 多項式譜系
多項式譜系其中 是在有 類中某些完備問題的預言機輔助的情況下,能在多項式時間內由圖靈機解決的決定性問題的集合。類別 也有類似的定義。比如, 是一些能在某些NP完全問題預言機的輔助下,在多項式時間內解決的問題的複雜度類。
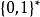 多項式譜系
多項式譜系(2)用存在狀態或者全稱狀態定義多項式譜系。令L為一個語言(或稱為決定性問題,即 的某個子集),p為某多項式,定義
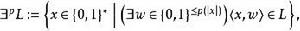 多項式譜系
多項式譜系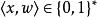 多項式譜系
多項式譜系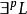 多項式譜系
多項式譜系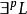 多項式譜系
多項式譜系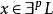 多項式譜系
多項式譜系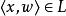 多項式譜系
多項式譜系其中 為某種將二進制字元串對x和w編碼為一個二進制字元串的標準編碼。 L代表一個有序的字元串對的集合,其中第一個字元串x是 的元素,而第二個字元串 w是一個足夠短的(長度不大於p(|x|))見證x在 內的字元串。換句話說, 若且唯若存在足夠短的見證字元串w使得 。類似地,定義
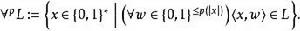 多項式譜系
多項式譜系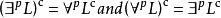 多項式譜系
多項式譜系注意到由德摩根定律得出 ,其中 L是L的補集。令C為一個語言集。延伸這些運算使得它們能夠套用於語言集上:
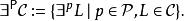 多項式譜系
多項式譜系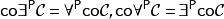 多項式譜系
多項式譜系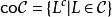 多項式譜系
多項式譜系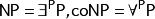 多項式譜系
多項式譜系其中P}為所有多項式的集合。同樣德摩根定律成立 ,其中 。 複雜度類NP和反NP可被定義為 , 其中P是所有可行的(多項式時間內的)遞歸語言。則多項式譜系可被遞歸定義為
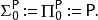 多項式譜系
多項式譜系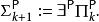 多項式譜系
多項式譜系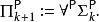 多項式譜系
多項式譜系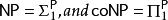 多項式譜系
多項式譜系注意 。這個定義反映出多項式譜系和算數階層之間的緊密關係。其中R和RE分別扮演了類似P和NP的角色。算數階層同樣是用一系列的實數子集來定義的。
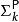 多項式譜系
多項式譜系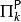 多項式譜系
多項式譜系(3)用交替式圖靈機的等價定義。定義 (或 )為從存在狀態(或全稱狀態)開始的{\displaystyle k}次交替式圖靈機能夠解決的問題的集合。
計算複雜性理論
計算複雜性理論(Computational complexity theory)是理論計算機科學和數學的一個分支,它致力於將可計算問題根據它們本身的複雜性分類,以及將這些類別聯繫起來。一個可計算問題被認為是一個原則上可以用計算機解決的問題,亦即這個問題可以用一系列機械的數學步驟解決,例如算法。
如果一個問題的求解需要相當多的資源(無論用什麼算法),則被認為是難解的。計算複雜性理論通過引入數學計算模型來研究這些問題以及定量計算解決問題所需的資源(時間和空間),從而將資源的確定方法正式化了。其他複雜性測度同樣被運用,比如通信量(套用於通信複雜性),電路中門的數量(套用於電路複雜性)以及中央處理器的數量(套用於並行計算)。計算複雜性理論的一個作用就是確定一個能或不能被計算機求解的問題的所具有的實際限制。
在理論計算機科學領域,與此相關的概念有算法分析和可計算性理論。兩者之間一個關鍵的區別是前者致力於分析用一個確定的算法來求解一個問題所需的資源量,而後者則是在更廣泛意義上研究用所有可能的算法來解決相同問題。更精確地說,它嘗試將問題分成能或不能在現有的適當受限的資源條件下解決這兩類。相應地,在現有資源條件下的限制正是區分計算複雜性理論和可計算性理論的一個重要指標:後者關心的是何種問題原則上可以用算法解決。
