均值保留展開式

均值保留展型（mean-preserving spread MPS） 在機率與數理統計中，均值保留展開型的意思是一個機率分布A變化到另外一個機率分布B,B的構成是將A的 機率密度函式 或者 機率質量函式（A's probability density function or probability mass function）展開成一個或者更多部分的形式，但是保持將均值（期望值）不變。正如此，MPS的意思也就是，根據它們的風險程度，提供了一種等均值機率分布的隨機排序方法。這種排序是偏序的（局部的partial），意味著對於兩個等均值的冒險行為（英文原為gambles），並不一定必要說，一個是另一個的MPS（this ordering is partial, meaning that of two equal-mean gambles, it is not necessarily true that either is a mean-preserving spread of the other）. 如果B是A的MPS的話，A可以說是B的均值收縮型。 利用MPS的冒險行為的排序（Ranking gambles by mean-preserving spreads）是二階隨機占優的特殊情況，也就是說，在等均值的特殊情況下，如果B是A的MPS，那么，A是B的二階隨機占優（A is second-order stochastically dominant over B）；如果A和B有相同的均值，那么反過來也成立。如果B是A的MPS，那么B具有比A更高的方差，且A和B的期望值是相同的;但是反過來並不一定成立，因為方差是一個完整的排序，而且通過MPS的排序僅僅是局部的（only partial） 。

相關命題

通過均值保留展開型進行的博彩（gamble）的排序是二階隨即占優的一個特例，有以下兩個命題

命題1：如果B是A的均值保留展開型，那么A是二階隨即占優B的。如果A與B具有相同的均值，那么上述命題的逆命題也成立。

命題2：如果B是A的均值保留展開型，那么B具有更高的方差，但是這個命題的逆命題不一定成立。因為方差是完全排序而通過均值保留展開則是偏序。

定義

X(A)與X(B)分別是博彩A和B的隨機變數，那么當前僅當X(B)與(X(A)+Z)具有同分布時，則B是A的均值保留展開型，其中Z有E(Z|X(A))=0的性質。

另一種寫法：

如果x(A)和x(B)是與冒險行為A和冒險行為B（gambles A and B）有關的隨機變數。如果x(B)與（x(A)+z）同分布，任意z滿足E(z|x(A))=0，那么B是A的MPS。

MPS還可以定義為累積分布函式FA和FB。如果A和B等均值，B是A的MPS，若且唯若F(A)以下的區域從負無窮到x，小於或等於F(A)以下的區域從負無窮到x，對於任意的實數x，在一些x嚴格不一樣。

這兩個數學定義可以拓展到同均值情況下的二階隨機占優。

示例

1 、 A的每一個結果A（ai）是具有相等的機率1/100,當i=1~50時，A(ai)=198；當i=51~100時，A（ai）= 202；

B的每一個結果B（ai）是具有相等的機率1/100,當i=1時， B(a1)=100； 當i=2~99時 ，B(ai)=200； 當i=100時，B（ai）=300.

由此可知E(A)=E(B).這種變化即可稱為均值保留展開型。

B是從A變形而來，將A中1%的數字，即從198變為100，把49%的數字，即將49個198變為200，再將1個202變為300，另外49個202變為200。這兩個MPS的的過程，是它自己的MPS，儘管98%的機率密度都移動到了均值（200）。

2、如右圖所示，對圖(a)所展示的密度函式進行均值保留，得到(b)的形狀。兩個分布具有相同的均值，但是圖(b)中，對於遠離均值的產出賦予更大的權重。

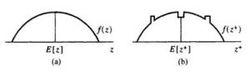示例2

相較關係

與期望效用理論的關係

如果B是A的MPS，那么A將是具有凹函式效用的效用最大化者的首選。反過來也成立，如果A和B有同均值，A是具有凹函式效用的效用最大化者的首選，那么B是A的MPS 。