簡介
地球自由振盪
free oscillations of the Earth
局部受到某種因素的激發時，地球整體產生的連續振動。地球在受到大地震、火山爆發或地下核爆炸的激發後，會發生整體的振動，並能持續一段時間。,這類地震與地球的固有振動有關。
由於地球很大，地球自由振盪的頻率很低，振動周期一般為數十秒至數十分鐘。通常振動亦很微弱，只有用靈敏的、可探測長周期振動的重力儀、應變地震儀和長周期地震儀等才能記錄到。大地震激發的地球長周期自由振盪往往延續幾天甚至幾個星期才會逐漸消失。人類對地球自由振盪的認識是從理論研究開始的。
歷史
地球自由振盪1829年法國人S.D.泊松最早研究完全彈性固體球的振動問題。此後的理論工作延續多年，20世紀地震學有了發展，使人類對地球內部構造有了更加清楚的認識，從而自由振盪的理論模式才比較接近真實地球。理論研究表明，自由振盪只能取一些特定的頻率，稱為地球的本徵頻率。與本徵頻率相應的振動叫做本徵振盪。每一種本徵振盪都對應一種駐波，是地球的一種諧振形式。本徵振盪分成兩類：①球型振盪。地球作球形振盪時，其質點位移既有徑向分量，也有水平分量。這是一種無旋轉振動。重力儀、應變地震儀和長周期地震儀均可記錄到這種振動。②環型振盪。地球作環型
1952 年11月4日堪察加大地震時，美國人H.貝尼奧夫首次在他自己設計製做的應變地震儀上發現周期約為57分鐘的長周期振動，經研究屬於地球的自由振盪。1960 年5月22日智利大地震時，貝尼奧夫和其他幾個研究集體都觀測到多種頻率的諧振振型。地球長周期自由振盪的真實性遂被最後證實。已觀測到的本徵頻率已達1000多個，其中球型振盪約占2/3，環型振盪約占1/3。
研究簡史
早在19世紀中葉,開爾文通過固體潮分析推算出剪下波在整個地球傳播一周約為68 min,這是人們對地球自由振盪本徵周期的首次推算.蘭姆在討論均勻彈性球體的動力學方程時發現了球型和環型自由振盪現象.Love研究了重力作用下可壓縮球體的靜態形變和小幅振動問題,並計算獲得了均勻地球模型的最長球型自由振盪周期約為60min。20世紀50年代以後,人們通過對地震體波和面波的走時分析,發現球形非旋轉球對稱各向同性彈性地球(SNREI)模型在一定精度範圍內是相當實用的.該模型由一組關於向徑r的密度函式ρ(r)、Lame係數λ(r)和彈性係數μ(r)來描述.Jobert利用Ray-leigh原理計算了地球自由振盪的本徵頻率(或本徵周期),也稱為自由振盪的簡正模,這是一項十分早期的工作.採用Bullen-B地球模型計算得到了環型自由振盪二階基頻簡正模0T2的周期為43.54 min.後來又採用同樣的方法得到球型自由振盪二階基頻簡正模為53 min，Jefferys等提出了利用Ray-leigh-Ritz展開法計算自由振盪簡正模，Takeu-chi採用這種展開法計算了地球環形振盪的球諧展開前三階低階簡正模,得到0T2為43.4 min。Al-terman等提出了一種簡潔的變數代換方式，將描述球型和環型自由振盪二階偏微分方程組轉化為一組常微分方程組,從而奠定了利用現代數值積分技術計算地球自由振盪本徵周期的基礎.基於均勻球對稱彈性球體模型,Pekeris等得到了描述球型和環型自由振盪的解析解形式，這些結果對於後來的研究,特別是在選擇數值積分所需的變數初值提供了有效參考意義，此後許多學者如Sato和Usa-mi,Takeuehi和Saito等都曾研究過地球自由振盪簡正模問題,較系統地研究了與數值積分有關的方向、變數在邊界面上的傳遞和處理,以及初值的選取等重要問題。
Benioff等在處理1960年5月22日的智利大地震期間的應變儀觀測資料時發現了地球自由振盪的長周期特徵.與此同時,Ness等在分析了同一地震期間拉科斯特彈簧型重力儀(LCR)觀測資料,得到了由地球自由振盪激發的類似長周期波.比較發現利用應變儀和重力儀觀測得到了許多類似的頻譜,測定周期也十分吻合.但進一步的比較發現,在應變儀資料中記錄到的一些頻譜沒有出現在重力觀測資料中.後來Pekeris指出Ness的重力結果中缺少的正是他在理論上計算獲得的環型振盪部分,而重力儀是記錄不到這種環型振盪的.因此由相應獨立的兩組觀測技術獲得的結果與理論計算的一致性證實了地球自由振盪現象的存在,同時揭開了這個地球物理學分支的帷幕.此後,不斷有報導獲得地球自由振盪現象的觀測結果.採用高解析度的譜分析技術,Dziewonski和Gilbert(DG)分析了阿拉斯加Ms8.5級地震期間全球84個地震台的觀測資料，獲得了十分重要的完整地球自由振盪觀測結果,這些結果一度曾被國際同行公認為是國際上最好的觀測結果,並在研究地球內部構造中發揮了重要作用。
我國學者也曾在地球自由振盪的數值計算方面作過研究。方俊討論了地球環型和球型自由振盪的數值計算問題,利用1066A地球模型分別獲得了一套本徵周期,討論了地球內部密度參數和彈性參數的變化對本徵周期的影響和由地心到地表(或由地表到地心)的數值積分方案。結果表明在基頻中僅0S2和0S3球型振型的振盪可穿透液態地核達到固態核心.另外傅承義等闡述了地球自由振盪滿足的基本彈性運動方程及其邊值條件,還討論了地球自由振盪的觀測及地球自轉和扁率對觀測頻譜的影響.郭俊義較詳細討論了從旋轉坐標系下的地球微小彈性運動方程推導地球自由振盪的常微分方程組的過程。
人類對地球自由振盪的認識是從理論研究開始的。1829年法國泊松(S.D. Poisson)最早研究了完全彈性固體球的振動問題。此後,英國的開爾文(Kel-vin)和達爾文(G.H.Darwin)也有重要貢獻。儘管理論工作延續多年,但只是在20世紀,地震學的發展使人類對地球內部構造的認識更加清楚以後，理論模式才比較接近真實地球。1952年11月4日堪察加大地震時,美國貝尼奧夫 (H.Benioff)首次在他自己設計製作的應變地震儀上發現周期約為 57分鐘的長周期振動。1960年5月22日智利大地震時，貝尼奧夫和其他幾個研究集體都觀測到多種頻率的諧振振型。地球長周期自由振盪的真實性遂被最後證實。至今已觀測到的本徵振盪頻率已達1000多個，其中球型振盪約占三分之二，環型振盪約占三分之一。圖1為由設在美國加利福尼亞伊沙貝拉台的應變地震儀記錄得到的兩個地震激發的地球自由振盪的功率譜密度曲線。δ是應變地震儀水平軸線同台站至震中大圓弧之間的夾角。
通過內引力計算，如果把地球作近似均勻考慮那么它自身固有振震周期，通過彈性微分方程可以計算到
只取彈性部分 X”=-3g(x/R) 非線性部分沒有計算，它不會影響周期與頻率的
得g(t) =-3gSIN(sqrt (3g/R)t) , sqrt() 表示平方根運算
周期T=2πsqrt (R/3g) 頻率f=1/T
平均長周期約為48分45秒，頻率為0.000341117HZ超低頻的。與長周期振動很接近，那么引起震盪的力可以認為是內部彈性引力引起的。
以上是通過近似計算的數據，如果考慮地球分層結構，通過計算它的不同層的震盪分別存在以下周期
下地幔57分44"與已經測量的長周期振動已經特別接近了，具體詳細以下圖，引力分段按彈性力計算。
地球自由振盪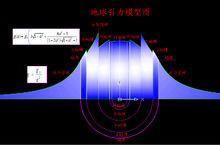
地球自由振盪理論
地球自由振盪的理論是在適當的定解條件下求解確定地球振動的微分方程組。方程組中包含 4個微分方程式，即：表示牛頓定律的動量守恆方程；表示質量守恆的連續方程；表示萬有引力定律的泊松方程；表示介質彈性的彈性方程。振動引起地球形變後必須滿足的定解條件是：①振動在地心處有限；②地球外表應力為零；③在地球表面和地球內部分界面上重力位及其梯度連續；④在地球內部的固體和固體間分界面上位移和應力連續；⑤在地球內部的固體和液體分界面上，法向位移連續，切向應力為零。通常是在以地心為原點的球極坐標系中用駐波法求上述問題的解。
滿足上述方程組和邊界條件的振動只能取一些特定的頻率，稱為地球的本徵頻率，相應的本徵角頻率通常用n ω嬓來表示，其數值取決於3個整數指標 n， l和 m。與本徵頻率相應的振動稱做本徵振盪。每一種本徵振盪都對應一種駐波,是地球的一種諧振形式。 n代表某一振型振動位移沿地球半徑方向的節點數; l-| m|表示位移在余緯方向的節點數（| m|≤ l）；2| m|表示位移在經度變化方向的節點數。 n最小時（0或1）的本徵頻率稱基頻，其餘稱諧頻。
本徵振盪分成兩類。一類叫球型振盪,通常用n S嬓表示。地球作球型振盪時，其質點位移既有半徑方向的分量，也有水平分量。這是一種無旋轉振動。重力儀、應變地震儀和長周期地震儀均可記錄到這種振動。另一類叫環型振盪，通常用nT嬒表示。地球作環型振盪時,各質點只在以地心為球心的同心球面上振動，位移無徑向分量，地球介質只產生剪下形變，無體積變化，地球的重力場不受擾動,重力儀記錄不到這種振盪。圖2繪出3種最簡單的振型0S孊、0S嬽和0T嬽的振動方式。振型 nT孊無意義，因為它表示地球各點位移恆為零。此外，地震及其他內力源激發不起。S嬒和0T嬼。0S嬒表示地球整體象剛體一樣在太空中振動，按動量守恆定律,任何內力都不能激發這種振動。0T嬼表示地球自轉角速度有變化，按角動量守恆定律，任何內力也都不可能激發這種振動。理論上，地球的諧振振型有無窮多個，實際的振動就是這無窮多個振型疊加的總結果。 對於球對稱的球體， n和 l相同而 m不同（ m=0，±1，±2，……± l，共2 l+1個）的振型都有相同的諧振頻率，這種情形稱為振型的簡併。地球的自轉效應使地球的振盪頻率對 m不再簡併。在振動的頻譜圖上，每條與某 n和 l相應的諧振譜線分裂為2 l+1條,它們等間距對稱地分布在 m=0譜線的兩側,這與原子光譜線在磁場中發生分裂的塞曼效應十分相似。自轉還會使質點振動方向發生像傅科擺一樣的變化，從而導致球型振盪與環型振盪發生耦合。真實地球並非球體，而是接近於旋轉橢球體。地球的橢率效應使頻譜線產生很微小的移動，造成分裂譜線的不對稱性。對低頻振型，自轉效應比橢率效應大得多；高頻振型反之。實際觀測中因有干擾，不易發現橢率效應。
套用
計算不同地球模式產生的自由振盪頻率，並與觀測頻率對比，可以檢驗並改善地球模式，從而研究地球內部的結構，與用地震體波研究地球內部結構的方法互為補充。測定相繼時間間隔內地球自由振盪頻譜譜峰的平均能量，或測定諧振譜峰的寬度（通常以能量降至譜峰能量的一半時相應的頻率變化來量度），可以研究振動能量在地球內部的衰減情況，並進而研究地球介質的非彈性性質。此外，根據給定的地球模式和嘗試的震源參數計算自由振盪的振幅和相位，然後與相應的觀測值對比，可以確定地震的震源參數。
