圓外切四邊形

四邊分別與圓相切的四邊形稱為圓外切四邊形。圓的外切四邊形的兩組對邊的和相等。

性質

圓外切四邊形

圓的外切四邊形的兩組對邊的和相等。同時，四邊形是圓外切四邊形的重要條件是四邊形的對邊和相等.

定理證明可利用切線長定理.

四邊形是圓外切四邊形的充要條件是該四邊形被其對角線所分成的四個小三角形的四個內心共圓.

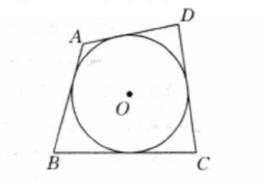
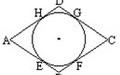
如圖，四邊形ABCD外切於00．則AB+CD=AD+BC ．

圓外切四邊形

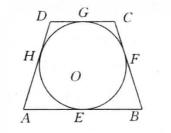圓外切四邊形

特殊舉例

圓外切四邊形是平行四邊形只有兩種情況：

1.圓外切菱形

合併圖冊 ​圓外切四邊形

2.圓外切正方形

性質：圓可以外切於一個正 方形，也可以內接於一個正方形

對於圓來說，他與外邊的四邊形外切，對於四邊形來說，他與裡邊的圓內接.

相關定理

(1)圓的外切四邊形中，兩雙對邊之和相等．

(2)若四邊形兩雙對邊之和相等，則此四邊形外切於圓 ．