工作原理
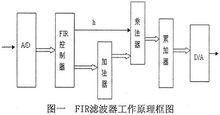FIR濾波器工作原理在進入FIR濾波器前，首先要將信號通過A/D器件進行模數轉換，把模擬信號轉化為數位訊號；為了使信號處理能夠不發生失真，信號的採樣速度必須滿足香農採樣定理，一般取信號頻率上限的4-5倍做為採樣頻率；一般可用速度較高的逐次逼進式A/D轉換器，不論採用乘累加方法還是分散式算法設計FIR濾波器，濾波器輸出的數據都是一串序列，要使它能直觀地反應出來，還需經過數模轉換，因此由FPGA構成的FIR濾波器的輸出須外接D/A模組。FPGA有著規整的內部邏輯陣列和豐富的連線資源，特別適合於數位訊號處理任務，相對於串列運算為主導的通用DSP晶片來說，其並行性和可擴展性更好，利用FPGA乘累加的快速算法，可以設計出高速的FIR數字濾波器。
硬體分類
FIR濾波器的硬體實現有以下幾種方式：
積體電路
一種是使用單片通用數字濾波器積體電路，這種電路使用簡單，但是由於字長和階數的規格較少，不易完全滿足實際需要。雖然可採用多片擴展來滿足要求，但會增加體積和功耗，因而在實際套用中受到限制。
DSP晶片
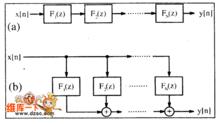FIR濾波器另一種是使用DSP晶片。DSP晶片有專用的數位訊號處理函式可調用，或者根據晶片指令集的結構自行設計代碼實現FIR的功能；由於FIR設計時其係數計算及其量化比較複雜，因此一般都採用MATLAB軟體作為輔助設計，計算出FIR的係數；然後進行代碼設計實現。實現FIR濾波器相對簡單，但是由於程式順序執行，速度受到限制。而且，就是同一公司的不同系統的DSP晶片，其編程指令也會有所不同，開發周期較長。
可程式
還有一種是使用可程式邏輯器件，FPGA/CPLD。FPGA有著規則的內部邏輯塊陣列和豐富的連線資源，特別適合用於細粒度和高並行度結構的FIR濾波器的實現，相對於串列運算主導的通用DSP晶片來說，並行性和可擴展性都更好。
特點
有限長單位衝激回響（FIR）濾波器有以下特點：
(1) 系統的單位衝激回響h (n)在有限個n值處不為零
(2) 系統函式H(z)在|z|>0處收斂，極點全部在z = 0處（因果系統）
(3) 結構上主要是非遞歸結構，沒有輸出到輸入的反饋，但有些結構中（例如頻率抽樣結構）也包含有反饋的遞歸部分。
設FIR濾波器的單位衝激回響h (n)為一個N點序列，0 ≤ n ≤N —1，則濾波器的系統函式為
H(z)=∑h(n)*z^-
就是說，它有（N—1）階極點在z = 0處，有（N—1）個零點位於有限z平面的任何位置。
基本結構
FIR濾波器有以下幾種基本結構：
橫截型
（7.10）式的系統的差分方程表達式為
y(n)=∑h(m)x(n-m) ( 7.11）
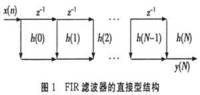
很明顯，這就是線性時不變系統的卷積和公式，也是x (n)的延時鏈的橫向結構，如圖4-11所示，稱為橫截型結構或卷積型結構，也可稱為直接型結構。將轉置定理用於圖4-11，可得到圖4-12的轉置直接型結構。
圖7.11 FIR濾波器的橫截型結構
級聯型
將H (z)分解成實係數二階因子的乘積形式
（7.12）
其中[N/2]表示取N/2的整數部分。若N為偶數，則N—1為奇數，故係數B2K中有一個為零，這是因為，這時有奇數個根，其中複數根成共軛對必為偶數，必然有奇數個實根。圖7-13畫出N為奇數時，FIR濾波器的級聯結構，其中每一個二階因子用圖4-11的橫型結構。
這種結構的每一節控制一對零點，因而再需要控制傳輸零點時，可以採用它。但是這種結構所需要的係數B2k（I = 0，1，2，k，= 1，2，．．．，[N/2]）比卷積型的係數h (n)要多，因而所需的乘法次數也比卷積型的要多。
圖9.13 FIR濾波器的級聯型結構
頻率抽樣
在第三章中已說過，把一個有限長序列（長度為N點）的z變換H (z)在單位圓上作N等分抽樣，就得到H (k)，其主值序列就等於h (n)的離散傅立葉變換H (k)。那裡也說到用H (k)表示的H (z)的內插公式為
（7.13）
這個公式就為FIR濾波器提供了另外一種結構，這種結構由兩部分級聯組成。
（7.14）
其中級聯的第一部分為
(7.15）
這是一個FIR子系統，是由N節延時單元構成的梳狀濾波器，令
則有
即Hc (z)在單位圓上有N個等間隔角度的零點，它的頻率回響為
（7.16）
因而幅度回響為
幅角為
其子網路結構及頻率回響幅度見圖7.14。
級聯的第二部分為
它是由N個一階網路並聯組成，而這每一個一階網路都是一個諧振器
（7.17）
令H'k(z)的分母為零，即令
可得到此一階網路在單位圓上有一個極點
圖7.14 梳狀濾波器結構及頻率回響幅度
圖7.15 FIR濾波器的頻率抽樣型結構
也就是說：此一階網路在頻率為
處回響為無窮大，故等效於諧振頻率為2πk / N的無損耗諧振器。這個諧振器的極點正好與梳狀濾波器的一個零點（I = k）相抵消，從而使這個頻率（ω= 2πk / N）上的頻率回響等於H (k)。這樣，N個諧振器的N個極點就和梳狀濾波器的N個零點相互抵消，從而在N個頻率抽樣點上（ω= 2πk / N，k = 0，1，．．．，N —1）的頻率回響就分別等於N個H (k)值。
N個並聯諧振器與梳狀濾波器級聯後，就得到圖7.15的頻率抽樣結構。
頻率抽樣結構的特點是它的係數H (k)就是濾波器在ω= 2πk / N處的回響，因此控制濾波器的頻率回響很方便。但是結構中所乘的係數H (k)及WN都是複數，增加了乘法次數和存儲量，而且所有極點都在單位圓上，由係數WN決定，這樣，當係數量化時，這些極點會移動，有些極點就不能被梳狀濾波器的零點所抵消（零點由延時單元決定，不受量化的影響）。系統就不穩定了。
為了克服係數量化後可能不穩定的缺點，可以將頻率抽樣結構做一點修正，即將所有零、極點都移到單位圓內某一靠近單位圓、半徑為r (r小於或近似等於1)的圓上（r為正實數）。
快速卷積
前一章談到，只要將兩個有限長序列補上一定的零值點，就可以用圓周卷積來代替兩序列的線性卷積。由於時域的圓周卷積，等效到頻域則為離散傅立葉變換的乘積。因而，如果
即將輸入x (n)補上L—N1個零值點，將有限長單位衝激回響h (n)補上L—N2個零值點，只要滿足L >= N1 + N2—1，則L點的圓周卷積就能代表線性卷積，即
用DFT表示，則有
Y(k) =X(k)H(k)
因而有
其中
Y(k) = DFT[y (n)]，L點
X(k) = DFT[x(n)]，L點
H(k) = DFT[h (n)]，L點
這樣，我們就可得到圖7.16的快速卷積結構，當N1，N2足夠長時，它比直接計算線性卷積要快得多。這裡計算DFY和IDFT都採用快速傅立葉變換計算方法。
音頻套用
隨著個人音頻的發展，曾經的IIR濾波器處理音頻帶來的音質劣化越來越受市場排斥。原有的IIR雖然具有簡單，算量小，使用方便的特點，但精度並不足夠，所以在專業音頻，很多有FIR 4096的音頻算法，例如拉脫維亞的Coneq等。
相反的WFIR濾波器
為彌補FIR在低解析度下低頻處理不佳，部分音頻算法使用了相反的WFIR濾波器。與FIR相反，WFIR對低頻處理較好，而對高頻無效。而每個工作點算量使用達到FIR的6倍。
FIR用於音頻的優勢
FIR的優勢在於可以無限增加精度（在足夠運算能力的前提下），並且不存在IIR濾波器的相位精度問題，是目前比較高端的解決方案
劣勢
1：因為採用的精度很高，所以對計算資源和記憶體、功耗的使用更高；
2：FIR在其他領域主要解決高頻問題，在音頻套用常常遇到1Khz以下的信號，FIR至少需要FIR 512才能對1K以下產生作用
3：過分運算，因為FIR每個處理單元寬度不能調整，因此在解決低頻問題時，高頻會出現過分運算的情況。
新的解決方案
包括FIR與IIR的混合使用，以及新型研發的音頻專用VIR濾波器。
