圓[一種幾何圖形]

在一個平面內，一動點以一定點為中心，以一定長度為距離旋轉一周所形成的封閉曲線叫做圓。圓有無數個點。

在同一平面內，到定點的距離等於定長的點的集合叫做圓。圓可以表示為集合{M||MO|=r},圓的標準方程是(x - a) ² + (y - b) ² = r ²。其中，o是圓心，r 是半徑。

圓形是一種圓錐曲線，由平行於圓錐底面的平面截圓錐得到。

圓是一種幾何圖形。根據定義，通常用圓規來畫圓。 同圓內圓的直徑、半徑長度永遠相同，圓有無數條半徑和無數條直徑。圓是軸對稱、中心對稱圖形。對稱軸是直徑所在的直線。 同時，圓又是“正無限多邊形”，而“無限”只是一個概念。當多邊形的邊數越多時，其形狀、周長、面積就都越接近於圓。所以，世界上沒有真正的圓，圓實際上只是概念性的圖形。

圓的定義

第一定義

在同一平面內到定點的距離等於定長的點的 集合叫做 圓（circle）。這個定點叫做圓的 圓心。

圓形一周的長度，就是圓的 周長。能夠重合的兩個圓叫 等圓，等圓有無數條對稱軸。

圓是一個正n邊形（n為無限大的正整數），邊長無限接近0但永遠無法等於0。

第二定義

平面內一動點到兩定點的距離之比（或距離的平方之比），等於一個不為1的常數，則此動點的軌跡是圓。

證明：點坐標為(x,y)與(x,y)，動點為(x,y)，距離比為k，由兩點距離公式。滿足方程(x-x)+ (y-y)= k×[ (x-x)+ (y-y)] 當k不為1時，整理得到一個圓的方程。

幾何法：假設定點為A，B，動點為P，滿足|PA|/|PB| = k（k≠1），過P點作角APB的內、外角平分線，交AB與AB的延長線於C，D兩點由角平分線性質，角CPD=90°。由角平分線定理：PA/PB = AC/BC = AD/BD =k，注意到唯一k確定了C和D的位置，C線上段AB內，D在AB延長線上，對於所有的P，P在以CD為直徑的圓上。

相關特點

徑

1.連線圓心和圓上的任意一點的線段叫做 半徑，字母表示為r（radius）

2.通過圓心並且兩端都在圓上的線段叫做 直 徑，字母表示為d（diameter）。直徑所在的直線是圓的對稱軸。

圓的直徑 d=2r

弦

1.連線圓上任意兩點的線段叫做 弦（chord）.在同一個圓內最長的弦是直徑。直徑所在的直線是圓的對稱軸，因此，圓的對稱軸有無數條。

弧

1.圓上任意兩點間的部分叫做圓弧，簡稱弧（arc）以“⌒”表示。
2.大於半圓的弧稱為優弧，小於半圓的弧稱為劣弧，所以半圓既不是優弧，也不是劣弧。優弧一般用三個字母表示，劣弧一般用兩個字母表示。優弧是所對圓心角大於180度的弧，劣弧是所對圓心角小於180度的弧。

3.在同圓或等圓中，能夠互相重合的兩條弧叫做 等弧。

角

1.頂點在圓心上的角叫做 圓心角（central angle）。

2. 頂點在圓周上，且它的兩邊分別與圓有另一個交點的角叫做 圓周角。圓周角等於相同弧所對的圓心角的一半。

圓周率

圓[一種幾何圖形]

圓周長度與圓的直徑長度的比值叫做 圓周率。它是一個無限不循環小數，通常用字母 表示，

圓[一種幾何圖形]

≈3.141592657......計算時通常取近似值3.14。我們可以說圓的周長是直徑的π倍，或大約3.14倍，不能直接說圓的周長是直徑的3.14倍。

形

1.由弦和它所對的一段弧圍成的圖形叫做 弓形。

2. 由圓心角的兩條半徑和圓心角所對應的一段弧圍成的圖形叫做 扇形（sector）。

表示方式

圓—⊙ ；半徑—r或R（在環形圓中外環半徑表示的字母）；圓心—O；弧—⌒；直徑—d ；

扇形弧長—L ； 周長—C ； 面積—S。

計算公式

圓的周長公式

圓[一種幾何圖形]

圓的周長： 圓周長的一半 c=πr

半圓的周長 c=πr+2r

圓的周長公式推導（此方面涉及到弧微分）

圓[一種幾何圖形]

圓[一種幾何圖形]

設圓的參數方程為，
圓在一周內周長的積分

圓[一種幾何圖形]

代入，可得

圓[一種幾何圖形]

圓[一種幾何圖形]

圓[一種幾何圖形]

圓[一種幾何圖形]

即

圓的面積公式

圓[一種幾何圖形]

圓[一種幾何圖形]

圓[一種幾何圖形]

圓[一種幾何圖形]

圓的面積計算公式： 或 或 圓的面積求直徑：

把圓分成若干等份，可以拼成一個近似的長方形。長方形的寬相當於圓的半徑。

圓[一種幾何圖形]

圓錐側面積 （l為母線長）

弧長角度公式

扇形弧長L=圓心角（弧度制）×R= nπR/180（θ為圓心角）（R為扇形半徑）

扇形面積S=nπ R²/360=LR/2（L為扇形的弧長）

圓錐底面半徑 r=nR/360（r為底面半徑）（n為圓心角）

扇形面積公式

R是扇形半徑，n是弧所對圓心角度數，π是圓周率，L是扇形對應的弧長。

也可以用扇形所在圓的面積除以360再乘以扇形圓心角的角度n，如下：

（L為弧長，R為扇形半徑）

推導過程:S=πr²×L/2πr=LR/2

(L=│α│·R)

位置關係

點和圓位置關係

①P在圓O外，則 PO>r。

②P在圓O上，則 PO=r。

③P在圓O內，則 PO<r。

反之亦然。

平面內，點P(x,y)與圓(x-a)²+(y-b)²=r²的位置關係判斷一般方法是：

①如果(x-a)²+(y-b)²<r²，則P在圓內。

②如果(x-a)²+(y-b)²=r²，則P在圓上。

③如果(x-a)²+(y-b)²>r²，則P在圓外。

直線和圓位置關係

①直線和圓無公共點，稱相離。 AB與圓O相離，d>r。

②直線和圓有兩個公共點，稱相交，這條直線叫做圓的 割線。AB與⊙O相交，d<r。

③直線和圓有且只有一公共點，稱相切，這條直線叫做圓的 切線，這個唯一的公共點叫做 切點。圓心與切點的連線垂直於切線。AB與⊙O相切，d=r。（d為圓心到直線的距離）

平面內，直線Ax+By+C=0與圓x²+y²+Dx+Ey+F=0的位置關係判斷一般方法是：

1.由Ax+By+C=0，可得y=（-C-Ax）/B，（其中B不等於0），代入x²+y²+Dx+Ey+F=0，即成為一個關於x的方程

如果b-4ac>0，則圓與直線有2個公共點，即圓與直線相交。

如果b-4ac=0，則圓與直線有1個公共點，即圓與直線相切。

如果b-4ac<0，則圓與直線有無公共點，即圓與直線相離。

2.如果B=0即直線為Ax+C=0，即x=-C/A，它平行於y軸（或垂直於x軸），將x²+y²+Dx+Ey+F=0化為（x-a）²+（y-b）²=r²，令y=b，求出此時的兩個x值x、x，並且規定x<x，那么：

當x=-C/A<x或x=-C/A>x時，直線與圓相離；

當x<x=-C/A<x時，直線與圓相交。

圓和圓位置關係

①無公共點，一圓在另一圓之外叫外離，在之內叫內含。

②有唯一公共點的，一圓在另一圓之外叫外切，在之內叫內切。

③有兩個公共點的叫相交。兩圓圓心之間的距離叫做圓心距。

設兩圓的半徑分別為R和r，且R〉r，圓心距為P，則結論：外離P>R+r；外切P=R+r；內含P<R-r；

內切P=R-r；相交R-r<P<R+r。

圓的性質

⑴圓是軸對稱圖形，其對稱軸是任意一條通過圓心的直線。圓也是中心對稱圖形，其對稱中心是圓心。

垂徑定理：垂直於弦的直徑平分這條弦，並且平分弦所對的2條弧。

垂徑定理的逆定理：平分弦（不是直徑）的直徑垂直於弦，並且平分弦所對的2條弧。

⑵有關圓周角和圓心角的性質和定理

① 在同圓或等圓中，如果兩個圓心角，兩個圓周角，兩組弧，兩條弦，兩條弦心距中有一組量相等，那么他們所對應的其餘各組量都分別相等。

②在同圓或等圓中，相等的弧所對的圓周角等於它所對的圓心角的一半（圓周角與圓心角在弦的同側）。

直徑所對的圓周角是直角。90度的圓周角所對的弦是直徑。

圓心角計算公式：　θ=(L/2πr)×360°=180°L/πr=L/r(弧度)。

即圓心角的度數等於它所對的弧的度數；圓周角的度數等於它所對的弧的度數的一半。

③ 如果一條弧的長是另一條弧的2倍，那么其所對的圓周角和圓心角是另一條弧的2倍。

⑶有關外接圓和內切圓的性質和定理

①一個三角形有唯一確定的外接圓和內切圓。外接圓圓心是三角形各邊垂直平分線的交點，到三角形三個頂點距離相等；

②內切圓的圓心是三角形各內角平分線的交點，到三角形三邊距離相等。

③R=2S△÷L（R：內切圓半徑，S：三角形面積，L：三角形周長）。

④兩相切圓的連心線過切點。（連心線：兩個圓心相連的直線）

⑤圓O中的弦PQ的中點M，過點M任作兩弦AB，CD，弦AC與BD分別交PQ於X，Y，則M為XY之中點。

（4）如果兩圓相交，那么連線兩圓圓心的線段（直線也可）垂直平分公共弦。

（5）弦切角的度數等於它所夾的弧的度數的一半。

（6）圓內角的度數等於這個角所對的弧的度數之和的一半。

（7）圓外角的度數等於這個角所截兩段弧的度數之差的一半。

（8）周長相等，圓面積比正方形、長方形、三角形的面積大。

相關定理

切線定理

圓[一種幾何圖形]

垂直於過切點的半徑；經過半徑的外端點，並且垂直於這條半徑的直線，是這個圓的切線。

切線的判定方法：經過半徑外端並且垂直於這條半徑的直線是圓的切線。

切線的性質：

（1）經過切點垂直於過切點的半徑的直線是圓的切線。

（2）經過切點垂直於切線的直線必經過圓心。

（3）圓的切線垂直於經過切點的半徑。

切線長定理

從圓外一點到圓的兩條切線的長相等，那點與圓心的連線平分切線的夾角。

以下簡述切線長定理的證明。

欲證AC =AB，只需證△ABO≌ △ACO。

設OC、OB為圓的兩條半徑，又∠ABO = ∠ACO=90°

在Rt△ABO和Rt△ACO中

∴Rt△ABO ≌ Rt△ACO（H.L）

∴AB=AC，且∠AOB=∠AOC，且∠OAB=∠OAC。

切割線定理

切割線定理的證明：

圓的一條切線與一條割線相交於p點，切線交圓於C點，割線交圓於A B兩點 ， 則有pC^2=pA·pB

設ABP是⊙O的一條割線，PT是⊙O的一條切線，切點為T，則PT²=PA·PB

證明：連線AT, BT

∵∠PTB=∠PAT(弦切角定理)

∠APT=∠TPB(公共角)

∴△PBT∽△PTA(兩角對應相等,兩三角形相似)

則PB：PT=PT：AP

即：PT²=PB·PA

割線定理

割線定理：從圓外一點引圓的兩條割線，這一點到每條割線與圓交點的距離的積相等。

一條直線與一條弧線有兩個公共點，我們就說這條直線是這條曲線的割線。

與割線有關的定理有：割線定理、切割線定理。常運用於有關於圓的題中。

與切割線定理相似：兩條割線交於p點，割線m交圓於A1 B1兩點，割線n交圓於A2 B2兩點，則pA1·pB1=pA2·pB2。

如圖直線ABP和CDP是自點P引的⊙O的兩條割線，求證：PA·PB=PC·PD

圓[一種幾何圖形]

證明：連線AD、BC∵∠A和

∠C都對弧BD

∴由圓周角定理，得 ∠DAP=∠BCP

又∵∠P=∠P

∴△ADP∽△CBP

（如果一個三角形的兩個角與另一個三角形的兩個角對應相等，那么這兩個三角形相似。）

∴AP:CP=DP:BP

即AP·BP=CP·DP

垂徑定理

垂直於弦的直徑平分這條弦，並且平分這條弦所對的兩條弧。

設在⊙O中，DC為直徑， AB是弦，AB⊥DC於點E，AB、CD交於E，求證：AE=BE，弧AC=弧BC，弧AD= 弧BD

連線OA、OB分別交⊙O於點A、點B

∵OA、OB是⊙O的半徑

∴OA=OB

∴△OAB是等腰三角形

∵AB⊥DC

∴AE=BE，∠AOE=∠BOE（等腰三角形三線合一）

∴弧AD=弧BD，∠AOC=∠BOC

∴弧AC=弧BC

弦切角定理

弦切角等於對應的圓周角。(弦切角就是切線與弦所夾的角）

已知：直線PT切圓O於點C，BC、AC為圓O的弦。

求證：∠TCB=1/2∠BOC=∠BAC

證明：設圓心為O，連線OC，OB,。

∵∠OCB=∠OBC

∴∠OCB=1/2*(180°-∠BOC)

又∵∠BOC=2∠BAC

∴∠OCB=90°-∠BAC

∴∠BAC=90°-∠OCB

又∵∠TCB=90°-∠OCB

∴∠TCB=1/2∠BOC=∠BAC

綜上所述：∠TCB=1/2∠BOC=∠BAC

圓的方程

1、 圓的標準方程：

在平面直角坐標系中，以點O（a，b）為圓心，以r為半徑的圓的標準方程是（x-a）+（y-b）=r。

特別地，以原點為圓心，半徑為r（r>0）的圓的標準方程為x+y=r。

2、 圓的一般方程：

方程x+y+Dx+Ey+F=0可變形為（x+D/2）+（y+E/2）=（D+E-4F）/4.故有：

圓[一種幾何圖形]

（1）當D+E-4F>0時，方程表示以(-D/2,-E/2)為圓心，以 為半徑的圓；

（2）當D+E-4F=0時，方程表示一個點（-D/2，-E/2）；

（3）當D+E-4F<0時，方程不表示任何圖形。

3、 圓的參數方程：

以點O（a，b）為圓心，以r為半徑的圓的參數方程是 x=a+r·cosθ, y=b+r·sinθ, （其中θ為參數）

圓的端點式：

若已知兩點A（a,b）,B（a,b），則以線段AB為直徑的圓的方程為 （x-a）（x-a）+（y-b）（y-b）=0

圓的離心率e=0，在圓上任意一點的曲率半徑都是r。

經過圓 x+y=r上一點M（a，b）的切線方程為 a·x+b·y=r

在圓（x+y=r）外一點M（a，b）引該圓的兩條切線，且兩切點為A,B，則A,B兩點所在直線的方程也為 a·x+b·y=r。

4、 圓的三點式方程：過不共線的三點A(x,y),B(x,y),C(x,y)的圓的方程為

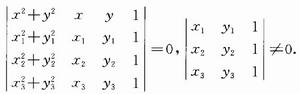圓的三點式方程

繪製方式

一般情況下可用圓規畫出圓形，或用一段繩子，一頭固定在地上，一頭轉，就能轉出圓，繩子越長，圓越大。

用AutoCAD繪圓

在AutoCAD“繪圖”下拉選單中，列出了6種“圓”的繪製方法，簡述如下：

（1）利用圓心和半徑繪圓：用滑鼠點取繪圖命令，然後根據提示操作；

（2）利用圓心和直徑繪圓：用滑鼠點取繪圖命令，然後根據提示操作；

（3）以兩點確定直徑繪圓：用滑鼠點取繪圖命令，然後根據提示操作；

（4）以三點確定直徑繪圓：用滑鼠點取繪圖命令，然後根據提示操作；

（5）以確定半徑與兩個圖形對象相切繪圓：用滑鼠點取繪圖命令，然後根據提示操作。

richtext控制項繪圓

定義一個數組，該數組用來存儲一個或多個坐標（Point）

然後按照以下步驟來實現

1 生成一個控制項（如Label）,並調整相應的屬性

2 在記憶體中建立一張臨時的圖像作為畫布，使用GDI+等各種繪圖,將圖像繪製到畫布上

3 將生成的控制項Image或BackGroundImage屬性值設定為步驟2生成的圖像

4 使用RichTextBox1.Controls.Add方法，將控制項添加進去（您可以指定它的坐標）

5 將當前已經添加的控制項的坐標記錄在數組中（如對應第1個數據）

6 添加RichTextBox1.Scroll事件代碼，在該代碼中，

圓

過獲取滾動條的值來計算已添加控制項應該所在的位置

說明：控制項可以通過代碼生成（推薦）

該方法與網上流傳的QQ聊天視窗內RichTextBox方法不同，

屬於簡單型

您務必要定義一個數組，用來參與ScrollBar滾動時，將目標控制項重新定位

歷史介紹

圓形，是一個看來簡單，實際上是十分奇妙的形狀。古代人最早是從太陽、陰曆十五的月亮得到圓的概念的。在一萬八千年前的山頂洞人曾經在獸牙、礫石和石珠上鑽孔，那些孔有的就很像圓。到了陶器時代，許多陶器都是圓的。圓的陶器是將泥土放在一個轉盤上製成的。當人們開始紡線，又制出了圓形的石紡錘或陶紡錘。古代人還發現搬運圓的木頭時滾著走比較省勁。後來他們在搬運重物的時候，就把幾段圓木墊在大樹、大石頭下面滾著走，這樣當然比扛著走省勁得多。

約在6000年前，美索不達米亞人，做出了世界上第一個輪子——圓型的木盤。大約在4000多年前，人們將圓的木盤固定在木架下，這就成了最初的車子。

會作圓，但不一定就懂得圓的性質。古代埃及人就認為：圓，是神賜給人的神聖圖形。一直到兩千多年前我國的墨子（約公元前468-前376年）才給圓下了一個定義：圓，一中同長也。意思是說：圓有一個圓心，圓心到圓周的長都相等。這個定義比希臘數學家歐幾里得（約公元前330-前275年）給圓下定義要早100年。

任意一個圓的周長與它直徑的比值是一個固定的數，我們把它叫做圓周率，用字母π表示。它是一個無限不循環小數，π=3.1415926535……但在實際運用中一般只取它的近似值，即π≈3.14.如果用C表示圓的周長：C=πd或C=2πr.《周髀算經》上說"周三徑一"，把圓周率看成3，但是這只是一個近似值。美索不達來亞人在作第一個輪子的時候，也只知道圓周率是3。魏晉時期的劉徽於公元263年給《九章算術》作注時，發現"周三徑一"只是圓內接正六邊形周長和直徑的比值。他創立了割圓術，認為圓內接正多連形邊數無限增加時，周長就越逼近圓周長。他算到圓內接正3072邊形的圓周率，π= 3927/1250。劉徽把極限的概念運用於解決實際的數學問題之中，這在世界數學史上也是一項重大的成就。祖沖之（公元429-500年）在前人的計算基礎上繼續推算，求出圓周率在3.1415926與3.1415927之間，是世界上最早的七位小數精確值，他還用兩個分數值來表示圓周率：22/7稱為約率，355/113稱為密率。 在歐洲，直到1000年後的十六世紀，德國人鄂圖（公元1573年）和安托尼茲才得到這個數值。如今有了電子計算機，圓周率已經算到了小數點後五萬億位小數了。