定義介紹
設有線性方程組
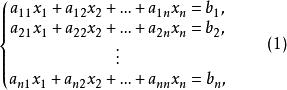回代過程或寫成矩陣形式
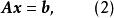回代過程其中
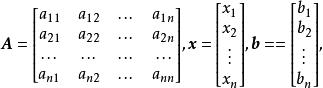回代過程設係數矩陣 A非奇異(即 A可逆)，即 A的行列式det( A)≠0，則式(1)有唯一解。
為了對高斯消去法有一個較清楚的了解，先看下列4個未知數的線性方程組的求解過程。
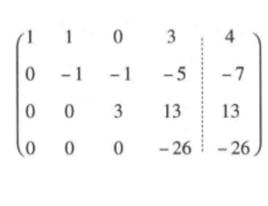
例1 求解線性方程組
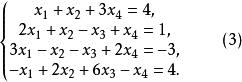回代過程
回代過程解： 消去法的第1步是用式(1)的第1個方程消去其餘方程中的未知數，這可分別將第1個方程的-2倍、-3倍和1倍加到第2個~第4個方程上，得
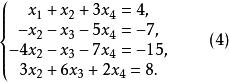回代過程
回代過程第2步是利用式(4)的第2個方程將第3、第4個方程中的未知數消去。為此，可將第2個方程的-4倍和3倍分別加到第3個、第4個方程上，得
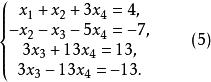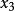回代過程
回代過程第3步是利用式(5)的第3個方程將第4個方程的中的未知數消去。為此，可將第3個方程的-1倍加到第4個方程上，得
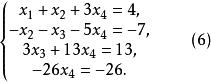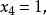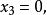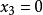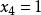回代過程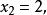
回代過程
回代過程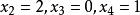
回代過程
回代過程
回代過程
回代過程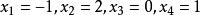
回代過程
回代過程到此為止， 消元過程結束。並且可以從式(6)的最後一個方程解出將其代入第3個方程可解出再將和代入第2個方程解出最後，將代入第1個方程解出。這樣就完成了對式(3)的求解，其解為。
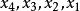回代過程以上求解線性方程組的過程稱為 順序高斯消去法，其中，利用加減消元法將一般方程組式(3)化為係數矩陣為上三角矩陣的上三角形方程組式(6)的過程稱為 消元過程，而由式(6)依次求出稱為 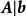回代過程。
回代過程一般地，順序高斯消去法主要包含消元和回代兩個過程。消元過程就是對式(1)的增廣矩陣()做有限次的初等行變換，使它的係數矩陣部分變為上三角矩陣。所用的初等變換主要是用一個數乘以某一行加到另一行上。
求解方法
線性方程組的求解方法在科學計算中占有極其重要的地位。一方面，在工程技術領域，經常以線性方程組作為其基本模型，例如電學網路問題、熱傳導問題、質譜儀數據分析、CT圖像重建等；另一方面，在許多有效的數值方法中，求解線性方程組是其中的關鍵步驟，如樣條捅值法、矩陣特徵值問題、微分方程數值解法等，都離不開線性方程組的求解。
線性方程組的數值解法可分為直接法和疊代法兩大類方法。直接法的特點是，運用此類方法求解線性方程組時，如果計算過程中沒有舍人誤差，那么經過有限次四則運算就能求得式(1)的精確解。但由於實際運算中總有舍人誤差，因此直接法求得的解也只能是近似解。另一類是疊代法，它首先選取一組初值，再運用同樣的計算步驟，重複計算，求得近似解。由於這類方法中出現了極限過程，因此必須研究疊代過程的收斂性。
求解線性方程組的直接法包括高斯消去法及其變形、直接三角分解法；疊代法包括雅可比疊代法、高斯一塞得爾疊代法和鬆弛法。直接法的基本思想是利用方程組的變形，逐步將方程組轉化為一個簡單的、易於求解的特殊形式的線性方程組(如三角形方程組)，然後再求解這一特殊形式的同解線性方程組。高斯消去法便是通過消元過程將方程組約化成上三角形方程組而完成的。
