四分位差

四分位差（quartile deviation），也稱為內距或四分間距（inter-quartile range），它是上四分位數（QU，即位於75%）與下四分位數（QL，即位於25%）的差。計算公式為：Qd =QU-QL四分位差反映了中間50%數據的離散程度，其數值越小，說明中間的數據越集中；其數值越大，說明中間的數據越分散。四分位差不受極值的影響。此外，由於中位數處於數據的中間位置，因此，四分位差的大小在一定程度上也說明了中位數對一組數據的代表程度。四分位差主要用於測度順序數據的離散程度。對於數值型數據也可以計算四分位差，但不適合分類數據。四分位數是將一組數據由小到大（或由大到小）排序後，用3個點將全部數據分為4等份，與這3個點位置上相對應的數值稱為四分位數，分別記為Q1（第一四分位數）、Q2（第二四分位數，即中位數）、Q3（第三四分位數）。其中，Q3到Q1之間的距離的差的一半又稱為四分位差，記為Q。四分位差越小，說明中間部分的數據越集中；四分位差越大，則意味著中間部分的數據越分散。

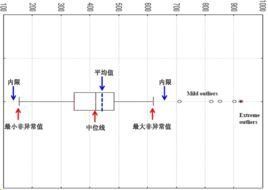
計算方法

如果所給的數據資料不同，四分位差的具體計算方法也不同：

1．未分組數據

首先對數據進行排序，求出Q、Q所在的位置；其次根據位置確定其對應的標誌值即Q、Q;最後計算二者差額的一半，即就是四分位差。

Q的位置= （n + 1) / 4

Q的位置= 3*（n + 1) / 4

2．單項式數列

先計算各組的累計次數，然後確定分位點位置。

Q的位置= Σf / 4

Q的位置= 3 * Σf / 4

對於上面的兩種情況，若(n+1)或Σf恰好為4的倍數，則計算出來的四分位數的位置就是整數，這時，各個位置上的變數值就是相應的四分位數；若(n+1)或Σf不是4的倍數，則按上面公式計算出來的四分位數的位次就可能帶有小數，這時可根據插值法來計算上下四分位數。再按公式計算出四分位差。

假設樣本容量為50時，=12．75，=38．25，則按插值法可得：

四分位差

整理得：Q=0．25X+0．75X

同樣可得：Q=0．75X+0．25X

3．組距式數列

先計算上、下四分位的值，然後再計算四分位差。此時計算四分位數的基本原理與中位數相類似。計算公式如下：

四分位差

式中，，，分別代表下四分位和上四分位數所在組的下限；，分別代表下四分位和上四分位數所在組以下的累計次數；，分別代表下四分位和上四分位數所在組的次數。

計算案例

例1：由7人組成的旅遊小團隊年齡分別為：17、19、22、24、25、28、34，求其年齡的四分位差。計算步驟為：

①計算Q，與Q的位置。

Q的位置= （n + 1) / 4 = （7 + 1) / 4 = 2

Q的位置= 3*（n + 1) / 4 = 3*（7 + 1) / 4 = 6

即Q與Q的位置分別為第2位和第6位。

②確定Q與Q的數值。

Q=19(歲)

Q=28(歲)

即第2位和第6位對應年齡分別為19歲和28歲。

③計算四分位差。

Q．D．=Q − Q=28-19=9(歲)

④含義。說明該旅遊小團隊有50%的人年齡集中在19～28歲之間，最大差異為9歲。

例2：根據某車間工人日產量分組資料，如表1所示，計算四分位差。

某車間工人日產量分組資料

按日產量分組（個）	工人數f(人）	向上累計工人數F(人）
5~10	12	12
10~15	46	58
15~20	36	94
20~25	6	100
合計	100	——

計算步驟為：

①確定Q與Q的位置。

Q的位置= Σf / 4 = 100 / 4 = 25

根據向上累計工人數可知Q在第2組即10～15內。

Q的位置= 3 * Σf / 4 = 3* 100 / 4 = 75

根據向上累計工人數可知，Q在第3組即15～20內。

②計算Q與Q的數值。

四分位差

③計算四分位差。

Q．D．=Q-Q=17．4-11．4=6(個)

④含義。計算結果表明，有50%(一半)工人的日產量分布在11．4～17．4之間，且最大差異為6個。

四分位差的優點表現為不受兩端各25%數值的影響，能對開口組數列的差異程度進行測度，可以衡量中位數代表性高低。缺點為不能反映所有標誌值的差異程度。