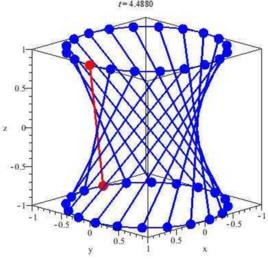
簡介
在幾何學中,單葉雙曲面(有時稱為鏇轉雙曲面或圓形雙曲面)是通過圍繞其主軸鏇轉雙曲線而產生的表面。 雙曲面是可以通過使用方向定標使其變形而從鏇轉拋物面獲得的表面。
雙曲面是二次曲面,其可以被定義為三個變數中的二維多項式的點的集合的表面。 在二次曲面中,雙曲面的特徵在於不僅具有對稱中心,而且讓平面和其相交還能形成錐體、柱體等。 雙曲面還具有三對垂直對稱軸和三對垂直對稱平面。
給定雙曲面,如果選擇軸為雙曲面對稱軸的笛卡爾坐標系,並且原點是雙曲面的對稱中心,則雙曲面可以由以下兩個方程之一定義:
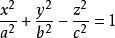 單葉雙曲面
單葉雙曲面或者
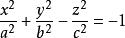 單葉雙曲面
單葉雙曲面這兩個方程均趨近於下面方程的錐。
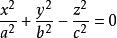 單葉雙曲面
單葉雙曲面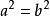 單葉雙曲面
單葉雙曲面若且唯若 時能形成鏇轉雙曲面。
在第一種情況下(方程式右側的為1),它是單葉雙曲面,也稱為雙曲面。 它是一個連線表面,每個點都具有負高斯曲率。 這意味著任何點處的切線平面與雙曲面相交成兩條線,因此單葉雙曲面是雙重曲面。
在第二種情況(方程式右側的為-1)中,它具有兩片雙曲面,也稱為橢圓雙曲面。 表面有兩個連線的部件,每個點都有正高斯曲率。 因此,在這個意義上,表面是凸的,每個點的切線平面僅在這一點上相交。
參數表示
可以定義雙曲面的笛卡爾坐標,類似於球面坐標,保持方位角θ∈[0,2π),但將傾斜度v變為雙曲線三角函式:
單葉雙曲面:v∈(-∞,∞)
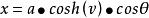 單葉雙曲面
單葉雙曲面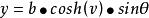 單葉雙曲面
單葉雙曲面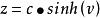 單葉雙曲面
單葉雙曲面屬性
表面上的線
(1)單葉雙曲面包含兩根線條。 這是一個雙重曲面。
(2)在a = b的情況下,單葉雙曲面是鏇轉表面,可以通過鏇轉兩條線l 或l ,它們偏向鏇轉軸。x(t)為:
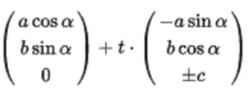 單葉雙曲面
單葉雙曲面平面部分
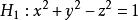 單葉雙曲面
單葉雙曲面為了簡單起見,設方程 。 因為一般雙曲面是單葉雙曲面,它的結果也適用於一般情況 。
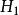 單葉雙曲面
單葉雙曲面(1)斜率小於1的平面(1是雙曲面上的線的斜率)與 相交形成橢圓;
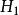 單葉雙曲面
單葉雙曲面(2)斜率等於1的平面(包含原點)與 相交形成一對平行線;
 單葉雙曲面
單葉雙曲面(3)斜率等於1的平面(不包含原點)與 相交形成拋物線;
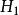 單葉雙曲面
單葉雙曲面(4)斜率大於1的非切向平面與 相交形成雙曲線。
雙曲面的對稱性
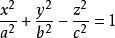 單葉雙曲面
單葉雙曲面雙曲面的方程:
(1)關於原點對稱;
(2)關於坐標平面對稱;
(3)在a = b(鏇轉雙曲面)的情況下,與z軸鏇轉對稱並對稱於包含z軸的任何平面。
雙曲面的曲率
單葉雙曲面的高斯曲率為負,兩片雙曲面的高斯曲率為正。 儘管它具有正曲率,但是具有另一適當選擇的度量的兩張雙曲面也可以用作雙曲線幾何的模型。
套用
由於有良好的穩定性和漂亮的外觀,單葉雙曲面常常套用於一些大型的建築結構,如發電廠的冷卻塔、電視塔等等(見 Hyperboloid structure)。
為迎接2010年亞運會而修建的 廣州電視塔(高度610m )的主體結構就是一個典型的單葉雙曲面(如圖)。
 單葉雙曲面
單葉雙曲面廣州電視塔
火電廠的冷卻塔常用的外形之一就是鏇轉單葉雙曲面,它的優點是對流快、散熱效果好。(詳見)
英國Didcot發電廠( Didcot Power Station) 的冷卻塔(Cooling Tower)
 單葉雙曲面
單葉雙曲面