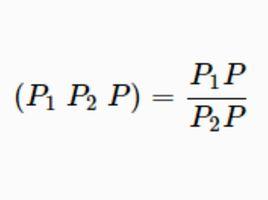算術中的比
基本介紹
比(ratio)亦稱單比，算術術語，比較兩個同類量之間的一種倍數關係，稱為這兩個同類量的比。在單位相同時，兩個量的比可以用表示這兩個量的數的比來代替。在實際中，只有同類量，且取同單位，才能相比。兩個量相比得到的倍數，稱為比值。兩個數相比，也可以說成是兩個數相除，a與b的比，記為a∶b或a/b，讀作a比b，符號“∶”稱為比號，比號前的數a，稱為比的前項，比號後的數b，稱為比的後項，比的後項不能是零。比的結果就是比值。儘管兩數相比的比值，相除的商和分數的值是相同的數，但比、除法及分數仍是有區別的，比是指兩個量的倍數關係，除法是一種運算，分數是一個數，比的基本性質是：比的前項和後項都擴大或縮小相同的倍數，比值不變，建立比的嚴格理論是歐多克索斯(Eudoxus，(C))，他引入了一個變數的概念，它不是整數，他認為整數是跳動的個體(即離散的)，而量是指線段、角、面積、時間等可以連續變動的東西，他用量這個概念建立了比和比例的理論，這樣就把有公度比和無公度比(比值為無理數)都包括進去了。歐幾里得(Euclid)《幾何原本》中的第五卷《比例論》，被認為是根據歐多克索斯的成果而編寫的，也是歐幾里得幾何的成就之一 。
單比與複比
單比單比是只包含兩項——前項和後項的比：a：b，或寫成。在四項比例式“a：b=c：d”中，等式每邊的比都是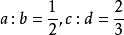單比。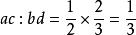
單比
單比複比是把兩個或多個單比的前項相乘積作前項，所有後項相乘積作後項，所作成的比，稱為原來幾個單比的複比。例如a：b與c：d是兩個單比，ac：bd就是複比。複比的比值，等於幾個單比值的乘積。例如，那么複比。
仿射幾何中的單比
基本概念
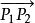單比
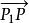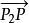單比
單比單比(simple ratio)亦稱仿射比，又稱簡單比，是仿射幾何中最基本的不變數。若P，P是有向直線上的兩個定點，P是這直線上的另一點，P分有向線段為兩個有向線段和，則其數量的比
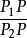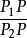單比 單比稱為三點P，P，P的 單比，記為(P P P)，即(PPP)=，其中P，P稱為 基點，P稱為 分點 。
顯然，當點P在點P，P之間時，單比(P P P)<0；否則(P P P)>0。
當點P與點P重合時，單比(P P P)=0；當點P與點P重合時，單比(P P P)不存在；當點P為線段PP的中點時，單比(P P P)=-1。
如果已知兩點P，P，且單比(P P P)為定值時，則點P在直線PP上的位置是被唯一確定的。
定理平行射影(透視仿射對應)保持共線三點的單比不變 。
交比
單比是仿射變換的基本不變數，但對於中心射影來說，單比不是不變數，它的基本不變數是交比。
下面介紹共線四點的交比的概念。
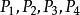單比
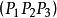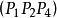單比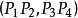
單比
單比定義 四個共線點的交比定義為兩個單比與的比，用符號表示，即
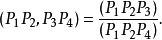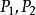單比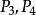
單比
單比其中叫做 基點偶；叫做 分點偶。
根據交比的定義有
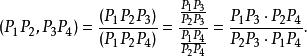單比交比又稱交叉比，複比 。
