單位矢量的引入
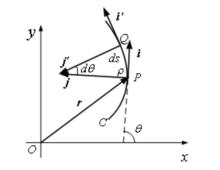 圖一 自然坐標系單位矢量的含義圖 質
圖一 自然坐標系單位矢量的含義圖 質如果質點沿著平面曲線C 運動,可以把加速度矢量a 分解為沿著軌道切線方向以及法線方向的兩個分量。設曲線C 上某一點為弧長坐標s 的原點O,沿軌道切線一方向運動時,軌道弧長s 增加,沿軌道切線另一方向運動時,軌道弧長s 減小。i 為沿軌道切線方向並指向軌道弧長s 增加的方向上的單位矢量, j 為沿軌道法向並指向曲線凹側的單位矢量,θ 為軌道前進的切線方向和x 軸之間的夾角,如圖一所示。i 、j 和dθ之間滿足下列關係式
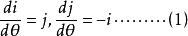 單位矢量
單位矢量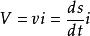 單位矢量
單位矢量 單位矢量
單位矢量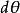 單位矢量
單位矢量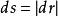 單位矢量
單位矢量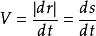 單位矢量
單位矢量弧長減小時,ds < 0。於是
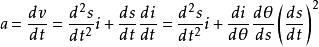 單位矢量
單位矢量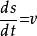 單位矢量
單位矢量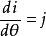 單位矢量
單位矢量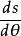 單位矢量
單位矢量 單位矢量
單位矢量 單位矢量
單位矢量因為 , ,,而此處則 等於曲線C 的曲率半徑 ,又因 恆大於0,
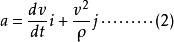 單位矢量
單位矢量故
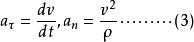 單位矢量
單位矢量質點沿曲線C 運動的切向和法向加速度分量分別為:
此式又稱為內稟方程。
自然坐標系單位矢量的新認識
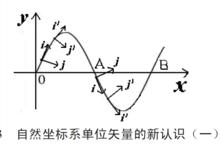 圖二 自然坐標系單位矢量的新認識(一)
圖二 自然坐標系單位矢量的新認識(一) 單位矢量
單位矢量 單位矢量
單位矢量 單位矢量
單位矢量在採用自然坐標系描述質點的平面曲線運動時,把加速度矢量a 分解為沿著軌道的切線以及法線方向兩個分量。其中,法線加速度的方向一定指向曲線在該點的凹側法線方向,這是由於質點法線方向受力的作用只改變質點速度的方向,而不改變質點速度的大小。在曲線的拐點處,法線加速度的大小為零。因此,法線方向的單位矢量 可以規定為沿軌道法向並指向曲線凹側。對於沿軌道切線方向的單位矢量i ,我們將證明其方向可以任意規定。單位矢量i 正向的選取不會影響加速度矢量在自然坐標系中的表達形式,即沿軌道切線方向不論怎么選取單位矢量的正向,加速度矢量在自然坐標系中的表達形式都如公式(2)所示。我們考慮質點沿著正弦曲線運動的情況,
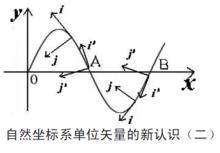 圖三 自然坐標系單位矢量的新認識(二)
圖三 自然坐標系單位矢量的新認識(二)如圖二和圖三所示。正弦曲線中既有凸的部分,也有凹的部分,同時還存在拐點。弧長坐標s 、單位矢量i 和j 的定義同上,θ 仍為軌道單位矢量i 的正向和x 軸之間的夾角。圖二 和圖三分別是沿軌道切線單位矢量i 正向選取的兩種情況。
 單位矢量
單位矢量綜上所述,單位矢量i 正向的選取不會影響加速度矢量a 在自然坐標系中的表達形式。事實上, dθ 、ds 的正負以及i 、j 和dθ 之間的關係式取決於曲線的凹凸性和單位矢量i 正向的選取。在自然坐標系中,對於常用到的一些關係式,比如曲線在某點的曲率半徑會根據dθ 、ds 的正負與ds / dθ 有相應的符號差別。此外,需要說明的是在靠近拐點時,ρ 趨於無窮大,法向加速度大小為零;又考慮到質點法線方向受力的作用只改變質點速度的方向,而不改變質點速度的大小,故在拐點兩側,法向單位矢量j 正向的突變對於求解質點曲線運動問題實質上沒有影響。
單位矢量正向的選取
自然坐標系
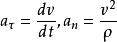 單位矢量
單位矢量理論力學中對沿曲線運動的質點, 常把其加速度矢量a 分解為沿軌道的切線方向和法線方向的兩個分量:.如果把軌道的切線和法線也作為坐標系來看,則叫自然坐標系。
選取方法
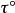 單位矢量
單位矢量切向坐標軸正向的選取:沿軌道曲線的切線,並指向弧坐標的正方向。
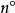 單位矢量
單位矢量法向坐標軸正向的選取:沿軌道曲線的主法線方向,即指向曲線的凹側。
注意:
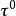 單位矢量
單位矢量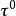 單位矢量
單位矢量( 1) 對於任意給定的光滑平面軌道曲線( 設曲線無拐點, 否則可分段考慮),在各點是唯一確定的,沿曲線是逐點連續變化的。
(2) 自然系正法向單位矢禪的方向與曲線的正法向( 指向曲率中心), 沿曲線各點處處相同。
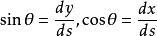 單位矢量
單位矢量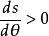 單位矢量
單位矢量( 3) 不僅保持兩式恆成立, 而且又有恆成立,
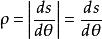 單位矢量
單位矢量於是就有恆成立。