1、問題連續體理論的源起
o 美國當時各種以“問題為中心”的教學改革風起雲湧。
o 倡導 “提出一個問題比解決一個問題更重要”
o “多元智慧型”理論的提出者霍華德·加德納認為：智慧型就是解決問題和製造產品的能力，認為能在複雜情境中解決複雜問題的人是具有最高智慧型的人”。
o 美國人斯克維在前人的基礎上首先提出問題連續體理論，但只把問題分為三類。後來，亞利桑那大學的瓊.梅克等人基於他們對多元智慧型的研究，又增加了兩類問題，構成了問題“連續體”，被稱為“梅克—斯克維的問題類型連續體”或“DISCOVER問題連續體矩陣”。
2、問題連續體理論簡介
美國亞利桑那大學的梅克教授運用多元智慧型理論，18年來在美國及世界30多個國家和地區開展了“發現”(DISCOVER)項目實驗，創立了以開發學生潛能為目標的“問題體系”。這個體系以“問題”為中心，以“方法”為中介，以“答案”為結果，根據學生的智力發展水平構建了五個層次的教學結構，揭示了五種類型的“問題解決”情景對於開發學生潛能的功能作用。“問題解決”教學已經成為各國各科教學改革的一個重要策略，更多地用於發展學生思維、探索、創新、實踐等能力。
問題連續體理論把問題按解決該問題所需的創造性的程度來劃分等級；即從教師和學生兩方面，就問題本身、解決問題的方法、答案這三個維度的已知或未知狀況;或從問題、方法、答案是唯一的, 系列的還是開放的這些不同層次，把問題分為五個類型。
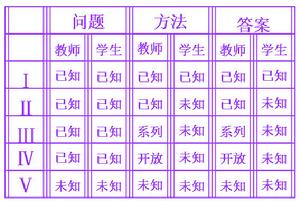問題連續體簡介從問題的性質看：
第一類型的問題，基本是事實水平的問題，通常是以了解個別範例的事實為目標，要求學生在對事實進行感知的基礎上解決問題；
第二類型的問題，仍然是事實水平的問題，但需進行必要的推理等思維活動方能解決問題；
第三類型的問題，是以形成概念、掌握規律或原理為目標，注意引導學生從個別擴展到“類”，再從“類”把握其背後的規律。學生不僅不需要完成抽象概括的過程，還要完成從系統化到具體化的過程。
第四類問題，運用所掌握的概念、規律或原理，把握該“範例”的上位主題，解決以主題範圍內的定向問題為目的，引導學生髮散思維，主動參與，互動合作，解決問題。
第五類問題，在主題範圍內自行發現與主題相關的綜合性問題，自行提出解決方案，解決問題，要求學生不僅提高解決真實問題的能力和創造性，同時要實現對人、對世界的態度、情感和價值觀。
第一類問題是完全封閉和收斂的，而第五類問題是完全開放和綜合的，所以的問題都處於這兩個極端之間，出現出“系列的、連續的”狀態，而不是相互隔絕、彼此獨立的！
從解決問題的方法看：第一類問題僅有一種方法，而第五類問題有無限種方法，在這兩個極端之間，解決問題的方法從一種到多種，再到無限種，呈現出多樣性和開放性。
從問題的結論看：第一類問題有著單一正確的結論，第五類問題通常是非常開放的，以至於也許有無數個可能的結論或根本就沒有正確的結論，具有高度的主觀性。對問題連續體來說，解決問題的結論也從一元到多元呈現出多樣性與開放性。

