簡介
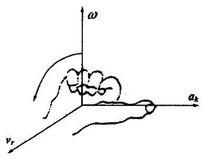 哥氏加速度
哥氏加速度哥氏加速度是由於相對運動與牽連轉動的相互影響而形成的。
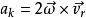 哥氏加速度
哥氏加速度哥氏加速度的表達式為:
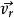 哥氏加速度
哥氏加速度式中: —質點相對運動速度
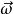 哥氏加速度
哥氏加速度—牽連角速度
如右圖所示,哥氏加速度的方向遵循右手螺旋定則。
基本推導
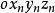 哥氏加速度
哥氏加速度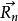 哥氏加速度
哥氏加速度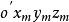 哥氏加速度
哥氏加速度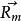 哥氏加速度
哥氏加速度如右圖所示,動點P相對於坐標系 的位置向量用 表示,相對於坐標系 的位置向量用 表示,轉換為具體坐標形式為:
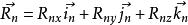 哥氏加速度
哥氏加速度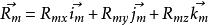 哥氏加速度
哥氏加速度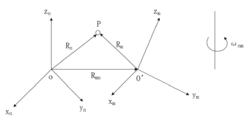 哥氏加速度
哥氏加速度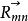 哥氏加速度
哥氏加速度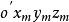 哥氏加速度
哥氏加速度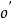 哥氏加速度
哥氏加速度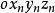 哥氏加速度
哥氏加速度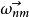 哥氏加速度
哥氏加速度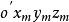 哥氏加速度
哥氏加速度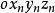 哥氏加速度
哥氏加速度設 為坐標系 的原點 和坐標系 的位置向量, 為 相對 的轉動角速度。
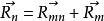 哥氏加速度
哥氏加速度由圖可知,
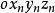 哥氏加速度
哥氏加速度兩邊同時對坐標系 取關於時間的導數得:
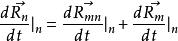 哥氏加速度
哥氏加速度式中第一項表示兩個坐標系之間的移動速度,第二項可寫成:
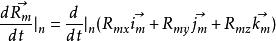 哥氏加速度
哥氏加速度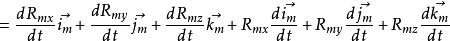 哥氏加速度
哥氏加速度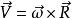 哥氏加速度
哥氏加速度根據繞定點轉動剛體一點的速度向量表示式 有:
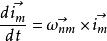 哥氏加速度
哥氏加速度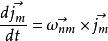 哥氏加速度
哥氏加速度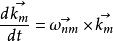 哥氏加速度
哥氏加速度由此得
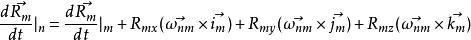 哥氏加速度
哥氏加速度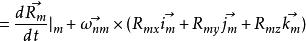 哥氏加速度
哥氏加速度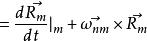 哥氏加速度
哥氏加速度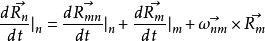 哥氏加速度
哥氏加速度即
再對上式左右兩邊關於時間取一次導數,即可得加速度之間的向量合成關係:
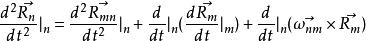 哥氏加速度
哥氏加速度同上述速度推導過程可知:
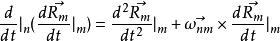 哥氏加速度
哥氏加速度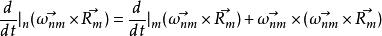 哥氏加速度
哥氏加速度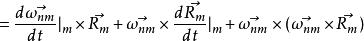 哥氏加速度
哥氏加速度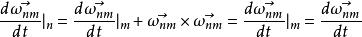 哥氏加速度
哥氏加速度注意到
故得到:
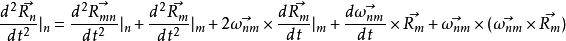 哥氏加速度
哥氏加速度上式等式右邊第三項即為哥氏加速度,第二項為相對加速度,第一、四、五項均為牽連加速度。
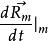 哥氏加速度
哥氏加速度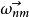 哥氏加速度
哥氏加速度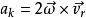 哥氏加速度
哥氏加速度為相對運動速度,為牽連角速度,由此得到哥氏加速度的一般表達式為:,方向遵循右手螺旋定則。
產生條件
哥氏加速度是由於由於相對運動與牽連轉動的相互影響而形成的,則其產生需滿足兩個條件:
1)動參考系存在牽連轉動,如果動參考系的牽連旋轉角速度為0,則不存在哥氏加速度;
2)動點存在相對運動,如果動點的相對速度為0,則也不存在哥氏加速度。