哈恩一巴拿赫定理

在泛函分析中，哈恩-巴拿赫定理是一個極為重要的工具。它允許了定義在某個向量空間上的有界線性運算元擴張到整個空間，並說明了存在「足夠」的連續線性泛函，定義在每一個賦范向量空間，使對偶空間的研究變得有趣味。這個定理以漢斯·哈恩和斯特凡·巴拿赫命名，他們在1920年獨立證明了這個定理。

哈恩一巴拿赫定理(Hahn-Banach theorem)   線性函式的延拓定理.哈恩一巴拿赫定理是線性泛函分析的基本定理，但它實際上與凸集分離定理等價，因而也可看做凸集分離定理的解析形式一般的哈恩-巴拿赫定理可以這樣來敘述:

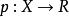哈恩一巴拿赫定理

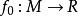哈恩一巴拿赫定理

定理   ：設X為實線性空間，M為它的線性子空間， 是X上的次可加正齊性泛函， 是M上的線性泛函，則

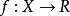哈恩一巴拿赫定理

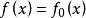哈恩一巴拿赫定理

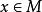哈恩一巴拿赫定理

（1）存在X上的線性泛函 使得 ，任意的 .

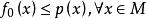哈恩一巴拿赫定理

哈恩一巴拿赫定理

（2）若 ，則可使 滿足

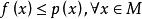哈恩一巴拿赫定理

一般泛函分析教科書中的X常取為賦范線性空間，p則取為空間的範數.這樣，哈恩一巴拿赫定理就變為線性泛函的保持範數不變的可延拓定理

前面已經提到，從選擇公理可以推出哈恩-巴拿赫定理。然而，反過來不成立。注意超濾子引理比選擇公理更弱，但從它也可以推出哈恩-巴拿赫定理（反過來則不行）。實際上，哈恩-巴拿赫定理還可以用比超濾子引理更弱的假設來證明。

對於可分空間|可分巴拿赫空間，Brown和Simpson證明了哈恩-巴拿赫定理可以從WKL——一個二階算術的弱子系統推出。