定義
哈密爾頓－凱萊定理
哈密爾頓－凱萊定理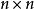
哈密爾頓－凱萊定理 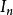哈密爾頓－凱萊定理 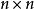哈密爾頓－凱萊定理明確地說：設 為給定的 矩陣，並設 為 單位矩陣，則 的特徵多項式定義為：
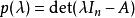哈密爾頓－凱萊定理其中 det 表行列式函式。凱萊-哈密頓定理斷言：
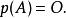哈密爾頓－凱萊定理凱萊-哈密頓定理等價於方陣的特徵多項式會被其極小多項式整除，這在尋找若爾當標準形時特別有用。
例子
舉例明之，考慮下述方陣：
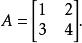哈密爾頓－凱萊定理其特徵多項式為
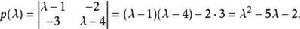哈密爾頓－凱萊定理此時可以直接驗證凱萊-哈密頓定理：
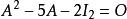哈密爾頓－凱萊定理此式可以簡化高次冪的運算，關鍵在於下述關係：
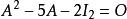哈密爾頓－凱萊定理
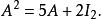哈密爾頓－凱萊定理例如，為了計算{\displaystyle A^{4}}，可以反覆利用上述關係式：
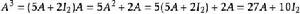哈密爾頓－凱萊定理
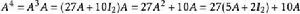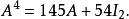哈密爾頓－凱萊定理
哈密爾頓－凱萊定理
哈密爾頓－凱萊定理或是，如果要計算 ，也可以假設：
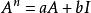哈密爾頓－凱萊定理
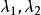哈密爾頓－凱萊定理然後，依照前面的特徵多項式之兩解 ，代入後可以得到
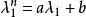哈密爾頓－凱萊定理
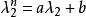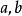哈密爾頓－凱萊定理
哈密爾頓－凱萊定理 哈密爾頓－凱萊定理然後解方程後求出 ，便可得 .
此外，凱萊-哈密頓定理也是計算特徵向量的重要工具。
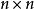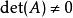哈密爾頓－凱萊定理 哈密爾頓－凱萊定理
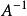哈密爾頓－凱萊定理
哈密爾頓－凱萊定理 哈密爾頓－凱萊定理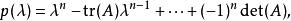
哈密爾頓－凱萊定理注：一般而言，若 矩陣 可逆（即： ），則 可以寫成 的冪次和：特徵多項式有如下形式
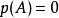哈密爾頓－凱萊定理 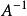哈密爾頓－凱萊定理
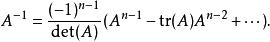哈密爾頓－凱萊定理將方程式 同乘以 ，便得到
定理證明
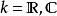哈密爾頓－凱萊定理以下考慮布於域 上的矩陣。
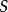哈密爾頓－凱萊定理 哈密爾頓－凱萊定理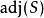
哈密爾頓－凱萊定理
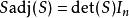哈密爾頓－凱萊定理凱萊-哈密頓定理可以視為線性代數中拉普拉斯展開的推論。拉普拉斯展開可推出若 是 矩陣，而 表其伴隨矩陣，則
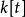哈密爾頓－凱萊定理
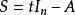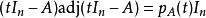哈密爾頓－凱萊定理
哈密爾頓－凱萊定理
哈密爾頓－凱萊定理取 ，便得到 。此式對所有 皆成立，由於實數或複數域有無窮多元素，上式等式在多項式環內成立。
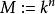哈密爾頓－凱萊定理 哈密爾頓－凱萊定理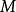
哈密爾頓－凱萊定理 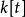哈密爾頓－凱萊定理
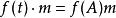哈密爾頓－凱萊定理
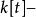哈密爾頓－凱萊定理
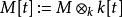哈密爾頓－凱萊定理 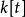哈密爾頓－凱萊定理設 ，矩陣 賦予 一個 -模結構： 。考慮 模 ，我們有 -模之間的“求值態射”：
哈密爾頓－凱萊定理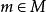
哈密爾頓－凱萊定理
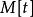哈密爾頓－凱萊定理固定 ，對 中的等式
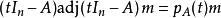哈密爾頓－凱萊定理
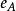哈密爾頓－凱萊定理
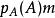哈密爾頓－凱萊定理 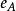哈密爾頓－凱萊定理
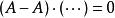哈密爾頓－凱萊定理右側取 後得到 ，左側取 後得到 。明所欲證。
一個簡單的證明： 令：
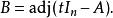哈密爾頓－凱萊定理 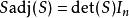哈密爾頓－凱萊定理由:
得：
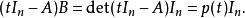哈密爾頓－凱萊定理
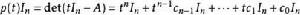哈密爾頓－凱萊定理因兩多項式，他們的對應項係數相等得：
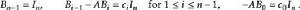哈密爾頓－凱萊定理在等式兩邊t的i次項係數分別乘以A, 並將等式左右兩邊分別相加併合項得：
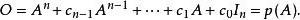哈密爾頓－凱萊定理得證.
抽象化與推廣
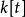哈密爾頓－凱萊定理
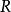哈密爾頓－凱萊定理 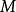哈密爾頓－凱萊定理前述證明用到係數在 的矩陣的克萊姆法則，事實上該法則可施於任何係數在交換環上的矩陣。藉此，凱萊-哈密頓定理可以推廣到一個交換環 上的任何有限生成自由模 （向量空間是特例）。中山正引理的一種證明就用到這個技巧。
