基本介紹
哈代不等式設 a=(a，a，…，a…)是給定的無窮維向量，記A=0，=0．對於n=1，2，…，記
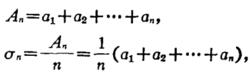哈代不等式
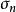哈代不等式{A}是級數∑a的部分和序列，而{}是序列{a}的算術平均序列．在級數理論中有這樣一個著名的定理。
哈代不等式
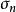哈代不等式 哈代不等式
哈代不等式
哈代不等式
哈代不等式 哈代不等式若，則．這就是說，a的收斂性是比的收斂性更強．哈代考慮了關於“屬於”的類似問題：若，即，則 σ=(σ，σ，…，σ…)是否也屬於，其中p>1?對這個問題哈代給出了肯定的回答並且獲得了下述精確的哈代(Hardy)不等式。
哈代不等式
哈代不等式定理1 設p>1，a是非負向量．那么當時，且成立著
哈代不等式或
哈代不等式其中等號僅當所有a=0時成立 。
哈代不等式的證明
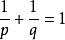哈代不等式證明當所有a=0時(1)顯然成立等號．我們設a≠0，先設a₁≠0，又設q是p的共軛數，即。
由於
哈代不等式所以有
哈代不等式
哈代不等式
哈代不等式
哈代不等式由楊格不等式得：
哈代不等式因此由（2）得：
哈代不等式
哈代不等式
哈代不等式
哈代不等式令得
哈代不等式
哈代不等式把他們都相加得
式（3）因此
式（4）利用漢竇不等式我們有
哈代不等式
哈代不等式把它同（4）相結合導出
哈代不等式
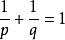哈代不等式 哈代不等式兩邊除以，然後兩邊p次方，注意到立即得到
哈代不等式
哈代不等式
哈代不等式令即知收斂並且
式（6）餘下還要指出(6)中等號不會成立．為此回到(4)和(5)，以∞代N得
式（7）
式（7）
哈代不等式
哈代不等式
哈代不等式
哈代不等式
哈代不等式由(6)，這裡的級數都是收斂的，由(7)兩邊除以後再p次方也得到(6)．因此當(6)成立等號時(7)也成立等號．由漢竇定理，當(7)中第二個等號成立時所有和成比例．由此導出(n=1，2，…)．因為且仃1=口1，故代入上式得五λ=1．這樣，有
哈代不等式
哈代不等式
哈代不等式
哈代不等式這除非，而這與收斂相矛盾．因此(7)不能成立等號．由此即知(6)也不能成立等式．這樣，我們在的假設下證明了定理。
哈代不等式
哈代不等式設都等於零，但(因為a≠0，這樣的s+1總存在)，其中s≥1．那么記
哈代不等式 哈代不等式的話，根據時的(1)式得到
哈代不等式
哈代不等式
哈代不等式
哈代不等式因為s≥1時，所以更有
式（8）
式8
哈代不等式
哈代不等式容易見到，(因為)上式左邊等於，右邊等於
哈代不等式因此（8）式就是
哈代不等式證畢。
哈代不等式順便指出，上述哈代不等式中的係數是最佳的，也就是說在這個不等式中不可能用比它更小的數去代替它 。
