同餘的基本性質(fundamental properties of con-gruences)同餘理論的重要內容之一關於同餘的基本性質，可分為如下三類:
1.同餘是一種等價關係，即具有自反性、對稱性和傳遞性.
2.同餘有四個與等式相類似的性質:
1)如果aba2,b:都是整數，而m是正整數，則當a}二b, (mod m ) ,aZ三b2 (mod m)都成立時，有al士az三b,士b2 (mod m).
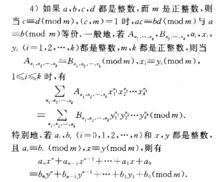同餘基本性質2)如果abaz,bZ都是整數，而m是正整數，則當a，三b,(modm),a:三b2 (mod m)都成立時，有a,aZ=b,bZ (mod m).
3)如果a,b,。都是整數，而m是正整數，則當a+b三c (mod m)時，有a三。一b (mod m).
3.同餘有五個與等式不相似的性質: 1)如果a,b都是整數，而k,m是正整數，則當a三b(mod m)成立時，有ak=bk (mod mk ).
2)如果“,b都是整數，d,m是正整數，d是a,b及m的任一公因數，則當a=b (mod m)成立時，有a/d=b/d (mod m/d ).
同餘基本性質3)如果a,b都是整數，d,m是正整數，且d}m,則當a=b(mod m)成立時，有a=b (mod d ).
5)如果a,b都是整數，而d,m是正整數，則當a=b (mod m)成立時，有(a,m)=(b,m)，若d能整除m及a,b中的一個，則d必能整除a,b中的另一個.
