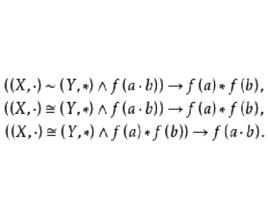基本定義
定義1
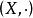 同構證明方法
同構證明方法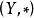 同構證明方法
同構證明方法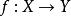 同構證明方法
同構證明方法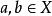 同構證明方法
同構證明方法設 和 是兩個同類型的代數系統(代數系統是集合及其運算構成的系統), 是一個映射,如果對於任意元 恆有
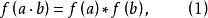 同構證明方法
同構證明方法 同構證明方法
同構證明方法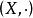 同構證明方法
同構證明方法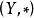 同構證明方法
同構證明方法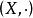 同構證明方法
同構證明方法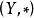 同構證明方法
同構證明方法 同構證明方法
同構證明方法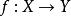 同構證明方法
同構證明方法 同構證明方法
同構證明方法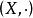 同構證明方法
同構證明方法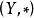 同構證明方法
同構證明方法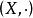 同構證明方法
同構證明方法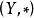 同構證明方法
同構證明方法 同構證明方法
同構證明方法則稱 是 到 的一個 同態映射,並稱 與 同態,用 表示;如果 是一個雙射,則稱 是 到 的一個 同構映射, 與 同構,用 表示 。
定義2
在證明中對如式(2)、式(3)、式(4)任意一命題的運用是 同構證 明方法:
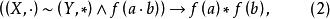 同構證明方法
同構證明方法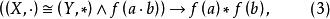 同構證明方法
同構證明方法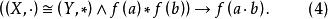 同構證明方法
同構證明方法舉例說明
例1 地圖(圖1)及圖上運算與實景及基於實景的運算構成的同構。
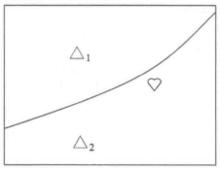 圖1 地圖
圖1 地圖 同構證明方法
同構證明方法一個地圖與實際場景的對應是典型的同構,如圖1所示。用兩個三角形符號△,△作為山的圖例,用曲線表示河流,用心臟的符號表示一尊佛像,這實際上建立了圖例(X集合)和實體(Y集合)的一一映射關係 。
 同構證明方法
同構證明方法:圖例→實景:
△→小山
△→大山
♡→佛像
在地圖上進行一種“找”的計算※,定義為“以它所計算的兩個元素的點(△,△)尋找等邊三角形的第三個點(♡)”。
在實地“找”的過程可以命名為一種計算■,定義為“定位和步行找到佛像”。
那么※和■就是完全不同的運算。在這種情況下,可以有如下推理:
 同構證明方法
同構證明方法 同構證明方法
同構證明方法 同構證明方法
同構證明方法 同構證明方法
同構證明方法 同構證明方法
同構證明方法 同構證明方法
同構證明方法 同構證明方法
同構證明方法 同構證明方法
同構證明方法 同構證明方法
同構證明方法 同構證明方法
同構證明方法 同構證明方法
同構證明方法(({△,△, (♡)},※) ({ (△), (△), (♡)},■)) ( (△※△)= (♡)→ (△)■ (△)= (♡) .
即同構方法使得通過圖例的計算可以在實景找到佛像目標 。
例2 兩個同構的群。
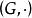 同構證明方法
同構證明方法將一個代數系統 稱為群,如果它:
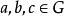 同構證明方法
同構證明方法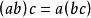 同構證明方法
同構證明方法(1)滿足結合率,即對任意的 ,有 ;
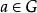 同構證明方法
同構證明方法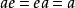 同構證明方法
同構證明方法(2)存在單位元,即對任意 ,有 ;
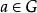 同構證明方法
同構證明方法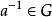 同構證明方法
同構證明方法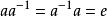 同構證明方法
同構證明方法(3)G中的任何一個元素都是可逆元,即對任意 ,都存在 ,使得 。
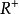 同構證明方法
同構證明方法 同構證明方法
同構證明方法設 為正實數的集合, 為實數的集合,×為乘法運算,+為加法運算。設存在函式:
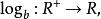 同構證明方法
同構證明方法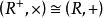 同構證明方法
同構證明方法其中:b是確定的底數。那么, ,因為
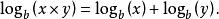 同構證明方法
同構證明方法